ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Хабаровский институт инфокоммуникаций (филиал)
Сибирский государственный университет
телекоммуникаций и информатики
Ряды Фурье
Хабаровск 2003
СОДЕРЖАНИЕ
1 Понятие периодической функции. Гармоники и тригонометрический ряд. 3
2 Скалярное произведение двух функций. ортогональночть и примеры ортогональных функций. Понятие полноты системы функций. 5
4 Ряд фурье для периодической функции периода 2l на [-l,l] по тригонометрической системе.Теорема дирихле о поточесной сходимости. 11
5 Ряд фурье по косинусам и синусам для периодической функции, периода l заданной на [0, l]. 14
6 Ряд фурье в комплексной форме для периодической функции периода 2l, заданной на [-l,l] 16
7 Ряд фурье для периодической функции периода 2π, заданной на отрезке [0, 2π] 18
8 Ряд фурье для четных и нечетных периодических функций периода 2l, заданных на [-l, l]. 19
9 Спектры периодических функций. 21
10 Преобразование фурье. Спектры непериодических функций. 24
11 Спектры типовых сигналов связи. 26
11.1 Спектр последовательности прямоугольных импульсов. 26
11.2 Спектр одиночного прямоугольного импульса. 29
11.3 Спектр колокольного (Гауссовского) импульса. 33
11.4 Спектр единичного импульса. 34
11.5 Спектр единичной функции. 35
11.6. Спектр одиночного импульса. 36
Список рекомендованной литературы.. 38
1 ПОНЯТИЕ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ. ГАРМОНИКИ И ТРИГОНОМЕТРИЧЕСКИЙ РЯД
В науке и технике часто приходится встречаться с периодическими явлениями, то есть такими, которые воспроизводятся в прежнем виде через определенный промежуток времени, называемый периодом. Примером может служить напряжение на выходе гармонических сигналов или генератора прямоугольных импульсов (рисунок 1.1).
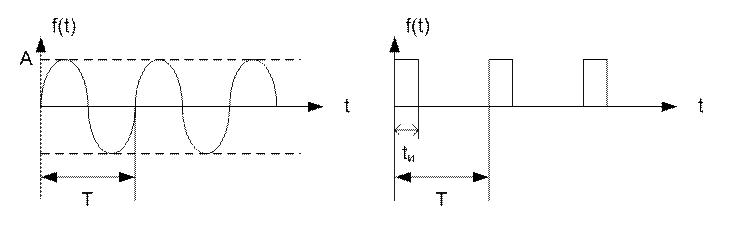 Рисунок 1.1
Рисунок 1.1
Определение.
Функция f(t) называется периодической (с
периодом T, если она задана на всей
числовой оси и для всех t ![]() выполняется
равенство:
выполняется
равенство:
![]() .
.
Например, тригонометрические функции
![]() имеют
период T=2π.
имеют
период T=2π.
Каждая же функция
cos kt, sin kt имеет период Т=![]() ,
для любого натурального k ≥
1.
,
для любого натурального k ≥
1.
Определение. Функция (периода T = 2l) вида
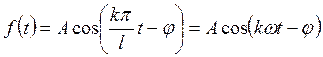 ,
(1)
,
(1)
где А>0, l>0 и φ – постоянные, K – натуральное число, называется гармоническим колебанием (с амплитудой А, начальной фазой φ и частотой kω) или гармоникой.
Число Т=![]() есть
период функции
есть
период функции ![]() ,
то есть одно полное колебание происходит за промежуток времени
,
то есть одно полное колебание происходит за промежуток времени ![]() . Число
колебаний за единице времени равно
. Число
колебаний за единице времени равно ![]() и
называется циклической частотой. Из подобных простейших периодических функций
могут быть составлены и более сложные. Например, если сложить несколько
гармоник вида
и
называется циклической частотой. Из подобных простейших периодических функций
могут быть составлены и более сложные. Например, если сложить несколько
гармоник вида
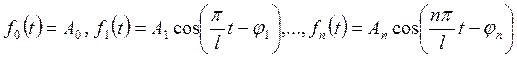 , которые имеют частоты
, которые имеют частоты
ω, 2ω, …, nω, ω = ![]()
и периоды
Т, ![]() ,
, ![]() , …,
, …, ![]() , Т = 2l, то получится функция с периодом T = 2l. Полученная функция уже существенно отличается от функций
типа (1).
, Т = 2l, то получится функция с периодом T = 2l. Полученная функция уже существенно отличается от функций
типа (1).
Наконец, более сложное периодическое колебание можно получить как сумму находящегося (при всех t) ряда
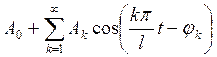 (2)
(2)
Заметим, что функции
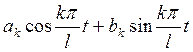
определяют гармоническое, потому что
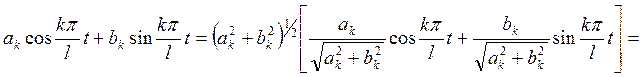
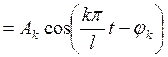 (3)
(3)
![]() ,
, 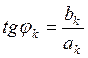 (4)
(4)
Из формул (3) – (2) получаем тригонометрический ряд в виде
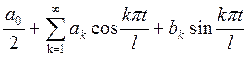 ,
(5)
,
(5)
где числа ![]() и
и ![]() называются
коэффициентами тригонометрического ряда. Ряды вида (5) и будут изучаться в
дальнейшем.
называются
коэффициентами тригонометрического ряда. Ряды вида (5) и будут изучаться в
дальнейшем.
Заметим, что выражение
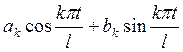
можно представить в виде
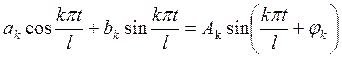 ,
, ![]() ,
, 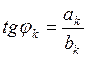 .
.
2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ФУНКЦИЙ. ОРТОГОНАЛЬНОЧТЬ И ПРИМЕРЫ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ. ПОНЯТИЕ ПОЛНОТЫ СИСТЕМЫ ФУНКЦИЙ.
Введем Необходимые для дальнейшего различные понятия.
Определение.
Функция ![]() называется
кусочно-непрерывной на [a,b], если она непрерывна на [a,b] за исключением конечного числа
точек разрыва первого рода.
называется
кусочно-непрерывной на [a,b], если она непрерывна на [a,b] за исключением конечного числа
точек разрыва первого рода.
Определение.
Точка ![]() называется
точкой разрыва первого рода для функции
называется
точкой разрыва первого рода для функции ![]() , если
односторонние пределы
, если
односторонние пределы ![]() ,
,
![]() конечны и
не равны.
конечны и
не равны.
Напомним, что в
пространстве трех измерений два вектора ![]() и
и ![]() называются
ортогональными, если их скалярное произведение равно нулю, то есть
называются
ортогональными, если их скалярное произведение равно нулю, то есть
![]() .
.
Если следовать
этой аналогии и функции ![]() ,
,
![]() считать
векторами, то мы должны определить СКАЛЯРНОЕ произведение для функций.
считать
векторами, то мы должны определить СКАЛЯРНОЕ произведение для функций.
Определение. Под
скалярным произведением двух кусочно-непрерывных функций ![]() и
и ![]() на [a,b] будем понимать число (f, g), равное
на [a,b] будем понимать число (f, g), равное
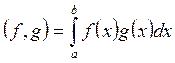 (2.1)
(2.1)
Множество всех кусочно-линейных функций, определенных на [a,b], для которых введено скалярное произведение по формуле (2.1), обозначим через Н(a,b).
Определение. Величина
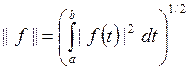
называется нормой
функции ![]() .
.
Определение.
Функция ![]() называется
нормированной, если
называется
нормированной, если
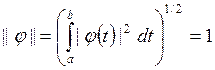
Две функции ![]() и
и ![]() называются
ортогональными, если их скалярное произведение равно нулю, то есть
называются
ортогональными, если их скалярное произведение равно нулю, то есть
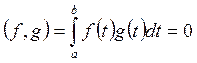 .
.
Определение. Система НЕПРЕРЫВНЫХ функций на [a,b]
![]() (2.2)
(2.2)
(Конечная или бесконечная) называется ортогональной, если функции имеют положительную норму и попарно ортогональны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.