Понятие периодической функции. Гармоники и тригонометрический ряд. Спектр последовательности прямоугольных импульсов, страница 6

Спектральное представление временных функций широко используется в теории связи. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используется различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательности прямоугольных и радиоимпульсов и т. д. Особо важную роль в теоретических исследованиях электрических цепей играют вычислительные сигналы в форме единичной функции  и импульсной функции  (функции Дирака). Определим спектры наиболее распространенных типовых сигналов.

11.1 Спектр последовательности прямоугольных импульсов

Пусть имеется периодическая последовательность импульсов прямоугольной формы периодом Т длительностью импульсов t_и и амплитудой А. Аналитическое выражение функции , описывающей импульс на отрезке , имеет вид

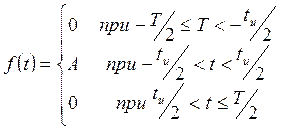                                                          (11.1)

График периодической последовательности импульсов изображен на рисунке 11.1.

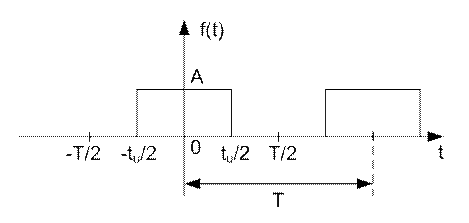
Рисунок 11.1

Данная функция является четной, так как ее график симметричен относительно оси ординат. Тогда коэффициенты Фурье это функции вычисляются по формулам (КФТ2), где .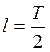

Итак,

                                                       

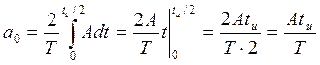
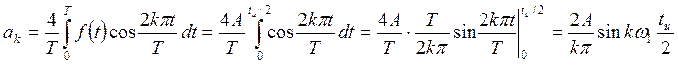  (11.2)

где .

Число 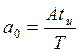 представляет собой среднее значение функции  за период и называется постоянной составляющей. Частоту  называют основной, или первой гармоникой, а частоты k высшими гармониками, где k=2,3,4,…

Построим амплитудный спектр рассматриваемой последовательности прямоугольных импульсов. Так как функция периодическая, то ее амплитудный спектр является линейчатым. Обозначим через  расстояние между любыми соседними гармониками. Очевидно, оно равно . Амплитуда k-ой гармоники согласно (11.2) имеет вид

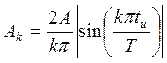                                                                                  (11.3)

Найдем отношение между периодом Т и длительностью импульса , при котором амплитуда k-ой гармоники обращается в нуль.

А₂≈32В, А₃≈15В, А₄≈0, А₅≈6,36В, А₆≈10,5В, А₇≈6,36В, А₈≈0, А₉≈4,95В, А₁₀≈6,37В.

Полученный в результате расчета амплитудный спектр приведен на рисунке 11.2.

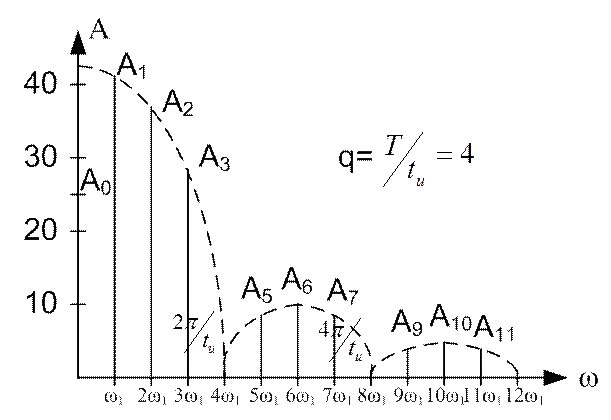
Рисунок 11.2

Такой спектр называют линейчатым или дискретным спектром.

Аналогично рассчитаны и построены спектры для q=8 и q=16. Они приведены на рисунках 11.3 и 11.4 соответственно.

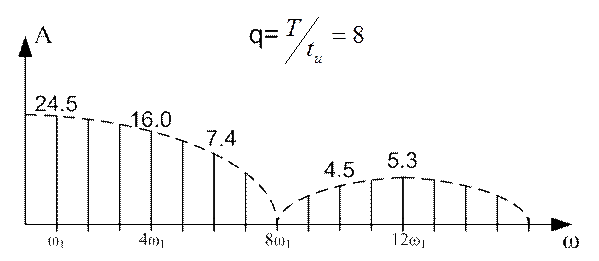
Рисунок 11.3

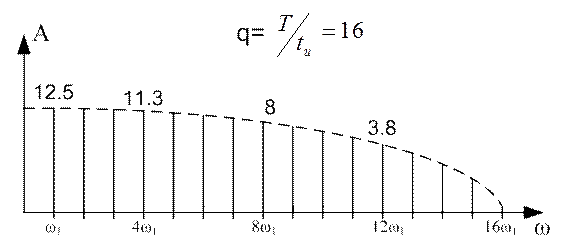
Рисунок 11.4

Из рисунка видно, что чем больше скважность прямоугольных импульсов, тем меньше значение имеет амплитуда первой гармоники, но тем медленнее убывает спектр.

11.2 Спектр одиночного прямоугольного импульса

Рассмотрим Ф (11.1) для случая, когда Т→∞, то есть периодическая последовательность импульсов вырождается в одиночный прямоугольный импульс, длительностью t_u.

Аналитическое выражение для этого импульса запишется в виде:

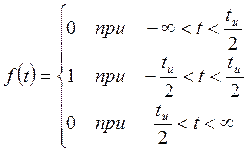
График этой функции изображен на рисунке 11.5.

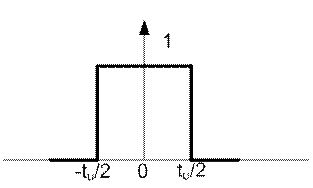
Рисунок 11.5

В этом случае частота первой гармоники и расстояние между гармониками становится равным 0, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга. Такой спектр называют сплошным. Отсюда следует важнейшее правило: периодические сигналы порождают дискретные спектры, а непериодические – сплошные (непрерывные).

Спектр прямоугольного одиночного импульса можно найти непосредственно из прямого преобразования Фурье (10.1)

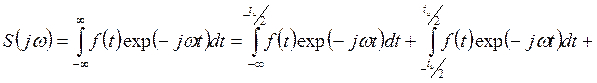
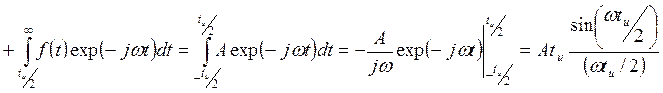(11.2)

Это будет пи условии, когд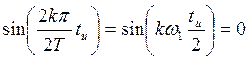а . Откуда 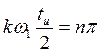. Таким образом номер k-ой гармоники 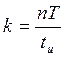 ( должно быть целым числом).

Величину 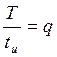 принято называть скважностью импульса.

Нетрудно видеть, что номер k-ой гармоники первый раз обращающейся в нуль, численно равен скважности.

Если q=2, то «первый нуль» приходится на вторую гармонику, нулевыми так же будут коэффициенты всех гармоник номера которых кратны двум, то есть 4й, 6й, 8й и так далее.

Аналогично при скважности q=3 нулевыми будут гармоники с номерами 3, 6, 9, 12, …, при q=4 не будет гармоник 4, 8, 12, …. По мере увеличения скважности (то есть уменьшения длительности t_u) первый нуль перемещается в область гармоник с большими номерами.

Пример: Рассчитать спектр сигналов прямоугольной формы со скважностью q=4 и амплитудой А=100 В для первых десяти гармоник.

Решение. Амплитуды составляющих для сигналов прямоугольной формы определяется из выражения (11.3).