Понятие периодической функции. Гармоники и тригонометрический ряд. Спектр последовательности прямоугольных импульсов, страница 2

Если система (2.2) ортогональна и  для всех k, то она называется ортонормированной.

Приведем ряд примеров ортогональных систем.

Определение. Система функций, определенных на , вида

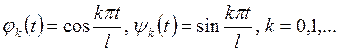                                                       (Т1)

называется тригонометрической системой функций.

Лемма 2.1. Система (Т1) тригонометрических функций ортогональна на .

Доказательство. Пусть, например,

.

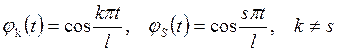Покажем, что

.

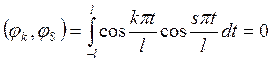Воспользуемся формулой

.

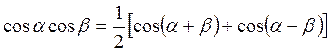Тогда

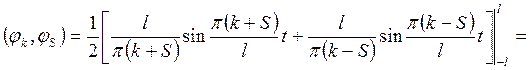
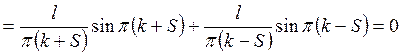
Итак,

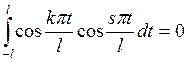,                                                                     (2.3)

Аналогично устанавливаются следующие равенства:

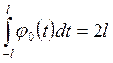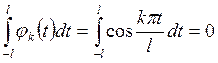, ,                                                     (2,4)

,

,

, .

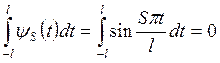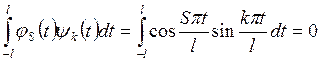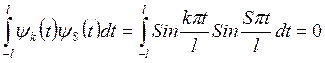Предлагаем самостоятельно доказать, что система (Т1) не ортогональна на отрезке .

Лемма 2.2. Системы функций

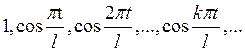                                                                       (Т2)

или

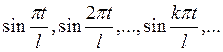                                                                           (Т3)

ортогональны на  каждая в отдельности.

Доказательство проводится по аналогии с леммой 2.1.

Предлагается доказать ортогональность систем (Т2) и (Т3) на , где α и β – целые числа.

Лемма 2.3. Система функций

, k=0,±1, ±2,…,                                                                     (Т4)

определенная на отрезке , ортогональная на этом отрезке.

Данное утверждение следует из равенства

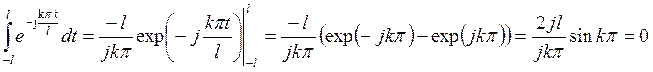
и того что

.

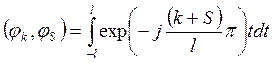Лемма 2.4. Система функций

                                                                         (Т5)

ортогональна на .

Отметим, что кроме перечисленных ортогональных систем (Т1) – (Т5) существуют и другие ортонормированные системы функций.

Определение. Ортогональная система функций  называется полной в , если каждая функция , для которой все скалярные произведения

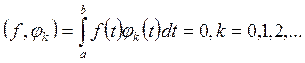
равны нулю, сама является нулевой функцией.

Теорема 2.1. Все ортогональные системы (Т1) – (Т5) являются полными на своей области определения.

3 СХОДИМОСТЬ В СРЕДНЕМ. РЯД ФУРЬЕ. СХОДИМОСТЬ РЯДА ФУРЬЕ В СРЕДНЕМЮ НЕРАВЕНСТВО БЕССЕЛЯ И РАВЕНСТВО ПАРСЕВАЛЯ

Рассмотрим тригонометрический ряд (1.5). Он является функциональным рядом. Составим n-ю частичную  сумму ряда

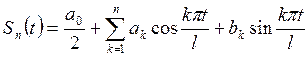                                                            (3.1)

Естественно поставить вопрос, в каком смысле будем понимать сходимость ? Будем рассматривать два вида сходимости: поточечную сходимость, которая определена в общей теории рядов и сходимость в среднем, определение которой приведем ниже.

Определение. Последовательность функций , принадлежащих Н (a,b), называется сходящейся в среднем к функции , если

                                                                                 (3.2)

Определение. Ряд функций 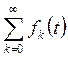 называется сходящимся в среднем к функции , если последовательность частичных сумм ряда 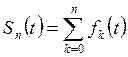 сходится к  в среднем.

Определение. Рядом Фурье функции  по ортогональной системе функций  называется функциональный ряд вида

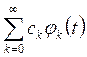                                                                                                    (Ф)

где коэффициенты Фурье считаются по формулам Фурье:

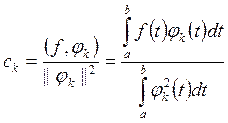, k = 0, 1, …                                                    (КФ)

Данный факт будем записывать следующим образом:

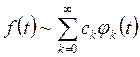                                                                                         (3.3)

Спрашивается, когда в соотношении (3.3) вместо ~ можно поставить знак =, понимаемое в определенном смысле?

Теорема 3.1. Пусть функция  кусочно-непрерывная на [a,b] и система функций  ортогональна и полна на [a,b]. Тогда ряд Фурье

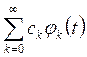                                                                                                  (3.4)

сходится в среднем к функции , то есть

,                                                                                 (3.5)

где

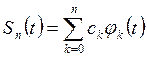.                                                                                      (3.6)

Рассмотрим величину . Она преобразуется следующим образом:

.

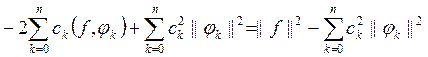Переходя к пределу при n→∞ и используя (3.5), получаем

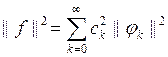                                                                                    (3.7)

Пусть система  ортонормированная, тогда из (3.7) получаем равенство Парсеваля

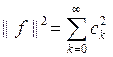
Из равенства Парсеваля очевидно следует неравенство

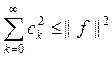, которое называется неравенством Бесселя.