Понятие периодической функции. Гармоники и тригонометрический ряд. Спектр последовательности прямоугольных импульсов, страница 5

Проводя аналогичные рассуждения для нечетной функции, получаем, что ряд Фурье для такой функции имеет вид

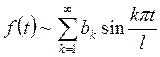,                                                                                    (8.5)

где

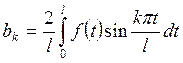                                                                                 (8.6)

Пример. Разложить в ряд Фурье 2l периодическую функцию: l=2

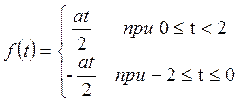
Решение. График заданной функции при а=const имеет вид

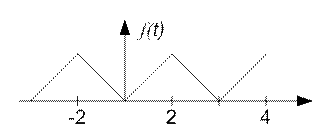
Рисунок 8.1

Данная функция четная, поэтому  согласно формул 8.3 имеем:

,

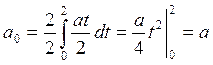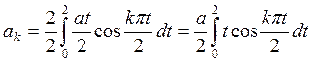
Интеграл берем по частям

, , ,

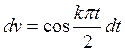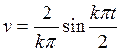
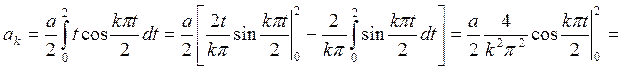
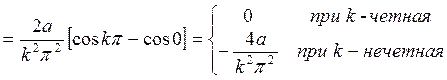
Получаем ряд

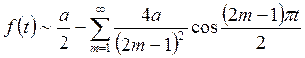
9 СПЕКТРЫ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ

Рассмотрим, например, периодическую функцию периода 2l, которая, вообще говоря, не является гармоническим колебанием. Пусть  задана на [-l, l] и является непрерывной. Тогда (см. пункт 4)

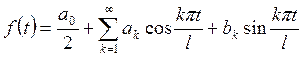, , где коэффициенты а₀ , а_k ,b_k находятся по формулам

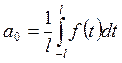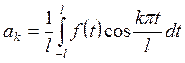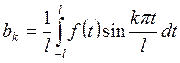 , ,                         (9.2)

В пункте 1 показано, что ряд (9.1) преобразуется к виде

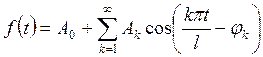                                                                   (9.3)

где

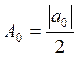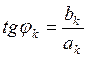, ,                                                            (9.4)

Итак, периодическая непрерывная на [-l, l] функция  представлена в виде ряда по гармоническим колебаниям (гармоникам) на отрезке [-l, l]

Определение. Набор чисел

,

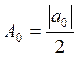называется амплитудным спектром периодической функции.

Амплитудный спектр можно изобразить графически. Возьмем ось частот ω и отложим на этой оси часты ω₀ = 0, 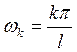, k=1, 2,… Против каждой  перпендикулярно оси откладываемы амплитуду А_n n-ой гармоники и получим частотный спектр в виде заборчика.

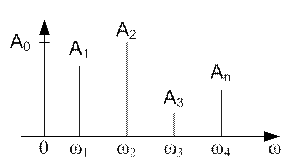
Рисунок 9.1

Определение. Набор чисел

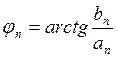, , n=1, 2, …

называется фазовым спектром периодической функции.

Фазовый спектр периодической функции можно также изобразить графически

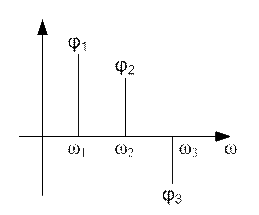
Рисунок 9.2

Теорема о стремлении коэффициентов Фурье к нулю.

Если функция  периода 2l кусочно-непрерывна и удовлетворяет на всей числовой оси неравенству

, , где M не зависит от t, то для коэффициентов Фурье справедливы соотношения:

,

Из этой теоремы вытекает, что амплитудный спектр периодической функции стремится к нулю.

Запишем ряд Фурье в комплексном виде

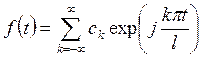,                                                               (9.5)

коэффициенты Фурье вычисляются по формулам

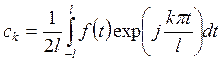 ,                                                     (9.6)

Набор чисел ,  называется амплитудным спектром периодической функции , а набор чисел  называется фазовым спектром этой функции.

Так как  и , то амплитудный и фазовый спектры симметричны относительно точки , то есть на графике это выглядит так:

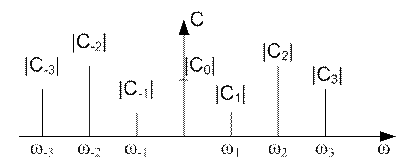
Рисунок 9.3

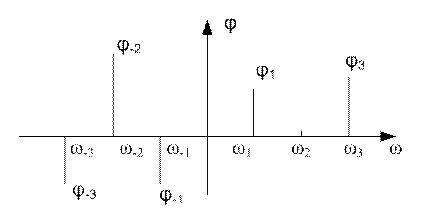
Рисунок 9.4

10 ПРЕОБРАЗОВАНИЕ ФУРЬЕ. СПЕКТРЫ НЕПЕРИОДИЧЕСКИХ ФУНКЦИЙ

Преобразованием Фурье функции , заданной на всей числовой оси, называется функция , определяемая равенством

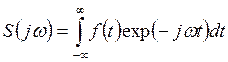 - прямое преобразование Фурье                (10.1)

Обратным преобразованием Фурье называется функция

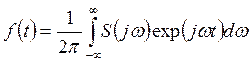                                                                   (10.2)

Эти два выражения (10.1) и (10.2) носят название пары преобразований Фурье. Они связывают между собой функцию времени  и комплексную функцию частоты .

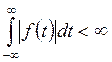Теорема. Если функция  абсолютно интегрируема на , то есть интеграл  сходится, то преобразование Фурье данной функции существует.

Если  равна нулю при , то преобразование Фурье такой функции получается из преобразования Лапласа путем замены на .

Наряду с преобразованием Фурье вводится понятие косинуса и синус-преобразование Фурье. Они определяются так:

,

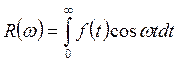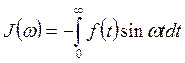
Функция  называется спектральной плотностью функции ,  называется модулем спектральной плотности или спектральной плотностью амплитуд.

Функцию спектральной плотности  запишем следующим образом:

Функция  называется спектральной плотностью фаз и

Пример. Найти спектральную плотность, модуль спектральной плотности и спектральную плотность фаз непериодической функции

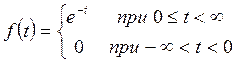
Решение. Спектральную плотность вычисляем по формуле (10.1)

.

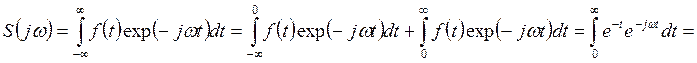
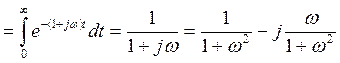Найдем модуль спектральной плотности :

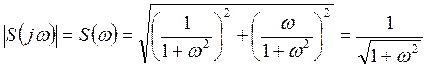
Спектральная плотность фаз :

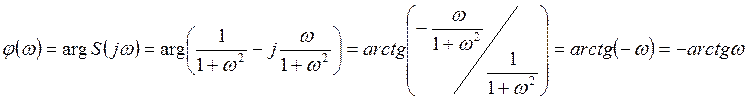
11 СПЕКТРЫ ТИПОВЫХ СИГНАЛОВ СВЯЗИ