Понятие периодической функции. Гармоники и тригонометрический ряд. Спектр последовательности прямоугольных импульсов, страница 4

Пример 1. Разложить в ряд Фурье периодическую функцию  периода , заданную следующим образом:

Решение. Согласно теории, данную функцию можно разложить либо в ряд по синусам, либо в ряд по косинусам. Найдем разложение по косинусам. Коэффициенты Фурье, согласно формул (КФТ2) равны

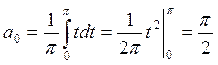
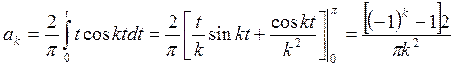
Второй интеграл вычисляется по частям.

Искомый ряд имеет вид

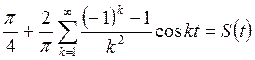
Согласно теореме Дирихле сумма ряда

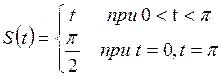
Пример 2. Разложить в ряд Фурье по синусам функцию , рассмотренную в предыдущем примере.

Решение. Коэффициенты Фурье находим по формулам (КФТ3):

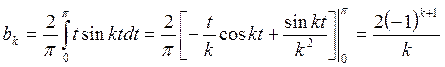
Ряд Фурье имеет вид

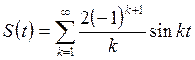
Предлагается самостоятельно найти сумму полученного ряда Фурье, используя теорему Дирихле.

6 РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ ДЛЯ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ ПЕРИОДА 2l, ЗАДАННОЙ НА [-l,l]

Пусть периодическая функция  периода 2l, заданная на [-l,l], является кусочно-непрерывной на [-l,l]. В пункте 2 указано, что система функции 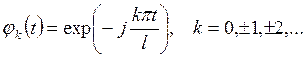(Т4)

                                                             (Т4)

является полной ортогональной системой функции на [-l,l]. Тогда, согласно теореме 3.1, для функции  можно построить ряд Фурье по системе (Т4). Он имеет вид

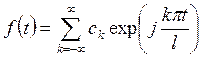                                                                           (ФТ4)

и данный ряд называется рядом Фурье в комплексной форме. По формуле (КФ) в данном случае коэффициенты Фурье имеют вид

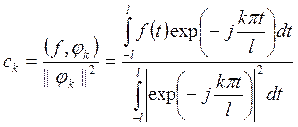                                                             (6.1)

Далее,

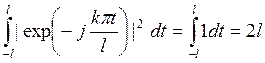
Отсюда и из (6.1) следует, что

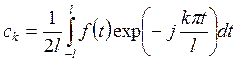                                                                   (КФТ4)

Задача 6.1. Сформулировать для ряда Фурье (ФТ4) теорему Дирихле.

Равенство Парсеваля для ряда (ФТ4) имеет вид

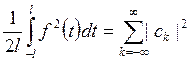
Пример. Разложить в комплексный ряд Фурье функцию периода 2π, заданную в виде

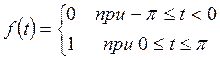
Решение. Вычислим коэффициенты Фурье данной функции по формулам (КФТ4). Имеем

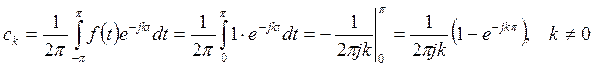
При k=0

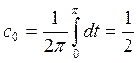
Получим ряд Фурье

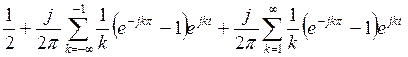
7 РЯД ФУРЬЕ ДЛЯ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ ПЕРИОДА 2π, ЗАДАННОЙ НА ОТРЕЗКЕ [0, 2π]

Пусть периодическая функция , заданная на [0, 2π], является кусочно-непрерывной на [0, 2π]. Полагая , мы можем построить ряды Фурье по системам (Т2) или (Т3) (см. пункт 5). С другой стороны система функций (Т5)

                                                                      (Т5)

является полной ортогональной системой функций на [0, 2π]. Тогда, согласно теореме 3.1, по данной системе (Т5) можно построить ряд Фурье, который сходится в среднем к функции . Данный ряд имеет вид

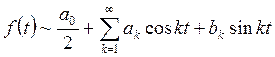                                                               (ФТ5)

коэффициенты Фурье вычисляются по формулам

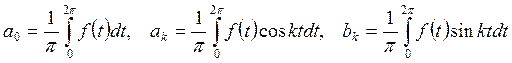                    (КФТ5)

Задача 7.1. Сформулировать теорему Дирихле для ряда (ФТ5).

Задача 7.2. Найти, чему равна сумма  ряда Фурье (ФТ5) в точках 0 и 2π.

Равенство Парсеваля для ряда ФТ5 имеет вид

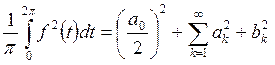
Пример. Разложить в ряд Фурье 2π – периодическую функцию

.

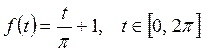Решение. Найдем коэффициенты Фурье:

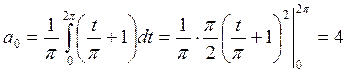
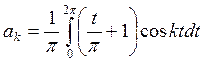
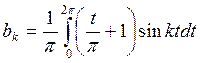
Интеграл берем по частям

, , ,

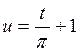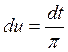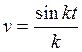
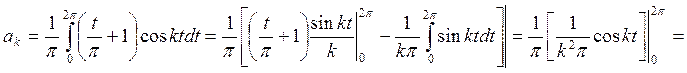
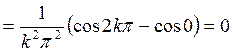
Аналогично найдем :

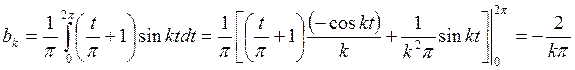
Искомый ряд

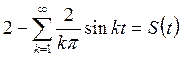
8 РЯД ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ ПЕРИОДА 2l, ЗАДАННЫХ НА [-l, l].

Сформулируем некоторые известные понятия для четных и нечетных функций.

Определение. Функция , заданная на всей числовой оси или на симметричном отрезке, [-l, l] называется четной, если , то есть ее график симметричен относительно оси ОУ, и нечетной, если , то есть ее график симметричен относительно начала координат.

Лемма 8.1. Если  четная функция на [-l, l], то

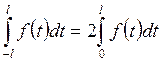                                                                                     (8.1)

Лемма 8.2. Если функция  нечетная на [-l, l], то

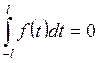                                                                                               (8.2)

Очевидно, что произведение двух четных или двух нечетных функций дают четную функцию. Произведение же четной и нечетной функции есть нечетная функция.

Пусть теперь  четная периодическая кусочно-непрерывная функция периода 2l задана на [-l, l]. Коэффициенты Фурье для такой функции считаются по формулам КФТ1 (см. пункт 4). Преобразуем их, используя леммы 8.1 и 8.2. Получаем

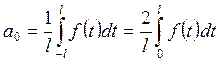
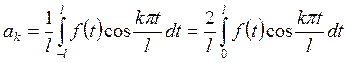                                                     (8.3)

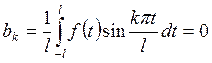
Тогда ряд Фурье для четной функции  имеет вид

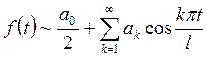,                                                                            (8.4)

а коэффициенты Фурье считаются по формулам (8.3).