Понятие периодической функции. Гармоники и тригонометрический ряд. Спектр последовательности прямоугольных импульсов, страница 7

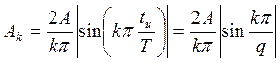
Для q=4, А=100 В будем иметь 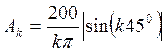 откуда

,

,

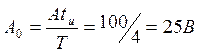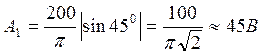Как известно, комплексная спектральная плотность  представима в виде:

, где  - спектральная плотность амплитуд, или амплитудный спектр,

 - фазовый спектр.

Используя Ф (11.2), получаем

Отсюда:

;

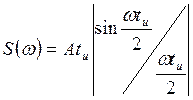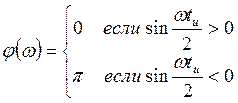
Графики амплитудного и фазового спектра одиночного прямоугольного импульса приведены на рисунке 11.6.

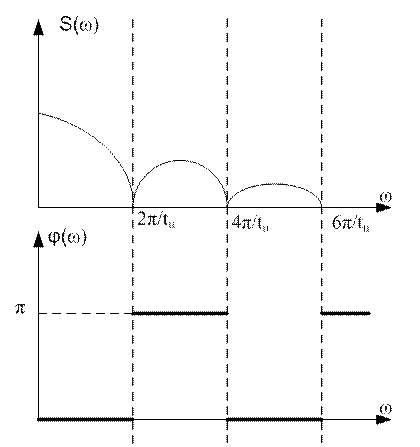
Рисунок 11.6

Из графиков видно, что спектральная плотность амплитуд обращается в ноль при 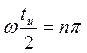, то есть при 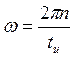. Замечаем, что при уменьшении длительности импульса t_u функция S(jω) растягивается, то есть ширина спектра увеличивается. Короткие сигналы имеют широкий спектр! Если ограничивать спектр прямоугольного импульса первым нулем спектральной плотности 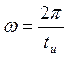, что справедливо на практике (так как в первом лепестке спектра сосредоточено 95% энергии всего сигнала), то для произведения длительности импульса  на ширину спектра.  получим

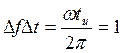
Это равенство является частным случаем более общего равенства, справедливого для всех импульсных сигналов

11.3 Спектр колокольного (Гауссовского) импульса.

Колокольным называется импульс, который описывается функцией

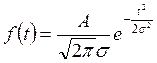
Комплексная спектральная плотность такого импульса:

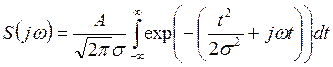
Откуда спектр амплитуд:

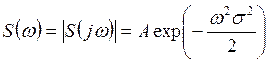
Графики колокольного импульса и его спектра показаны на рисунке 11.7 а и б соответственно.

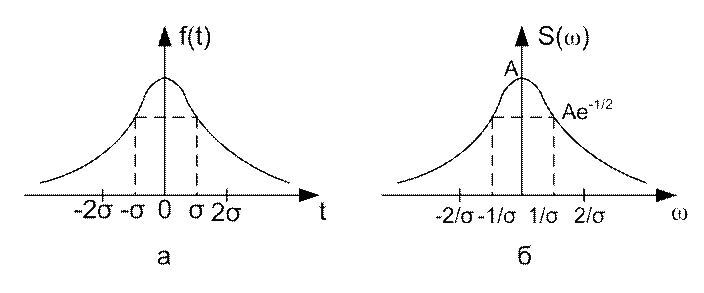
Рисунок 11.7

11.4 Спектр единичного импульса

Единичным импульсом или дельта-функцией  называется функция бесконечно-малой длительности с конечной площадью, равной единице (рисунок 11.8)

Такую функцию можно рассматривать, как предел прямоугольного импульса при  с длительностью  и амплитудой 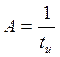. В этом случае согласно Ф (11.2) спектральная плотность единичного импульса S(jω) представима формулой

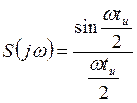
Устремляя  получаем . Это же результат можно получить и обычным способом, используя фильтрующие свойства δ-функции:

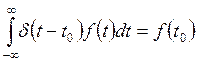, а именно

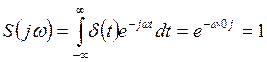
На рисунках 11.8 и 11.9 приведены графики δ-функции и  ее амплитудного спектра

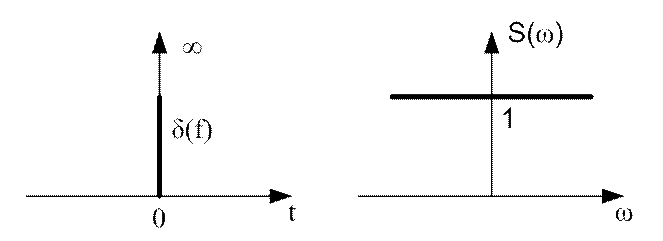
Рисунок 11.8                                    Рисунок 11.9

Из рисунка видно, что спектр δ-функции является сплошным и равномерным вплоть до бесконечно больших значений частоты.

Это подтверждает сделанный ранее вывод между длительностью импульса  и шириной его спектра .

Единичный импульс является математической абстракцией. Физически можно реализовать только очень короткий импульс с площадью равной q.

Спектр такого импульса определяется выражением

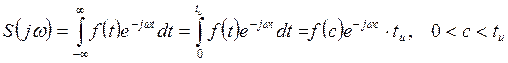
Так как 0<c<t_u – мало (вследствие малости значения t_u), то exp(-jωc)≈1 и тогда  - площади рассматриваемого импульса.

Таким образом короткий импульс любой формы имеет равномерный спектр вплоть до частот порядка  (пока выполняется условие . Далее спектральная плотность начинает убывать.

11.5 Спектр единичной функции

Единичная функция, единичный скачок, или функция включения (рисунок 11.10) записывается виде

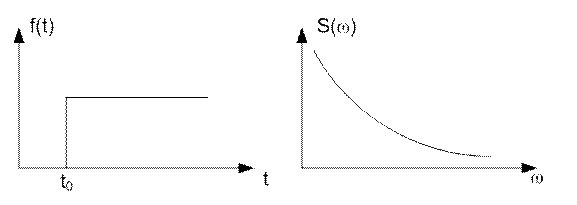
Рисунок 11.10                      Рисунок 11.11

Заметим, что рассмотренный ранее единичный импульс можно рассматривать как производную от единичной функции:

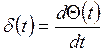
а единичную функцию как интеграл от δ – функции:

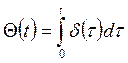
Спектральная плотность этой функции

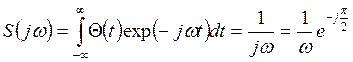
Модуль спектра этой функции

Зависимость его от частоты показана на рисунке 11.11.

11.6. Спектр одиночного радиоимпульса.

Радиоимпульсом называется импульс (рисунок 11.12), временная функция которого записывается в виде:

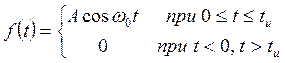
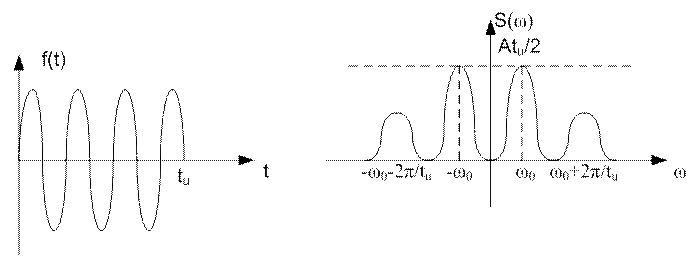
Рисунок 11.12                                        Рисунок 11.13

Спектральная плотность радиоимпульса будет равна:

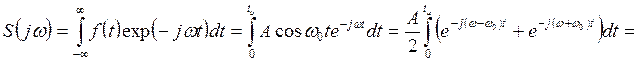
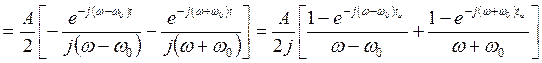
Откуда

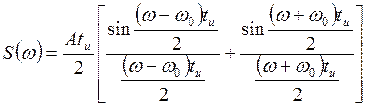
Сравнивая спектры одиночного видеоимпульса и радиоимпульса замечаем, что сгибающие их амплитуды спектров совпадают по форме, но спектр радиоимпульса сдвинут в область высоких частот на частоту ω₀.

Список рекомендованной литературы

1. Бугров Я. С., Никольский С. М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М: Наука. 1982 г.

2. Мантуров О. В. Курс высшей математики. М.: Высшая школа. 1991г.

3. Воробьев Н. Н. Теория рядов. М.: Наука. 1973 г.

4. Жевержеев В. Ф., Кальницкий Л. А., Сапогов Н. А. Специальный курс математики для ВТУЗов. М.: Высшая школа. 1970 г.

5. Романовский П. И. Ряды Фурье. Теория Поля. Аналитические и специальные функции. Преобразование Лапласа. М.: Наука. 1980 г.

6. Колобов А. М. Избранные главы высшей математики. М.:Высшая школа, 1965 г.

7. Бондарев Б. Н. Основы теории передачи сигналов. Н.: НЭИС, 1969г.