Вернемся к параграфу 2, где указано, что системы (Т1) – (Т5) являются полными ортогональными системами. Тогда, согласно теореме 3.1, по этим системам можно построить соответствующие ряды Фурье для кусочно-непрерывных функций, определенных на соответствующем отрезке. В этом случае достаточно научиться вычислять коэффициенты Фурье по соответствующей системе (Т1).
4 РЯД ФУРЬЕ ДЛЯ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ ПЕРИОДА 2l НА [-l,l] ПО ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЕ. ТЕОРЕМА ДИРИХЛЕ О ПОТОЧЕЧНОЙ СХОДИМОСТИ.
Пусть функция ![]() задана на
отрезке [-l,l]. Данную функцию можно продолжить на
всю числовую ось с периодом 2l. Обратно, если
задана на
отрезке [-l,l]. Данную функцию можно продолжить на
всю числовую ось с периодом 2l. Обратно, если ![]() -
периодическая функция периода 2l, то ее аналитическое задание (задание с помощью формул) достаточно знать
на [-l,l]. Этим фактом в последующих
параграфах мы и будем пользоваться.
-
периодическая функция периода 2l, то ее аналитическое задание (задание с помощью формул) достаточно знать
на [-l,l]. Этим фактом в последующих
параграфах мы и будем пользоваться.
Лемма 4.1. Если
функция ![]() является
периодической с периодом T, то
является
периодической с периодом T, то
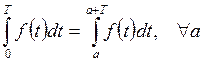
Данная лемма
позволяет вычислять коэффициенты Фурье функции ![]() по
системам (Т1) – (Т5) на соответствующем отрезке.
по
системам (Т1) – (Т5) на соответствующем отрезке.
Пусть ![]() -
периодическая функция периода 2l. Найдем коэффициенты Фурье данной функции, заданной на [-l,l] по тригонометрической системе (Т1)
-
периодическая функция периода 2l. Найдем коэффициенты Фурье данной функции, заданной на [-l,l] по тригонометрической системе (Т1)
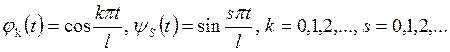
Коэффициенты ![]() по
функциям
по
функциям ![]() обозначим
через
обозначим
через ![]() , а по
, а по ![]() через
через ![]() . Согласно
формулы (КФ) (п.3) получаем
. Согласно
формулы (КФ) (п.3) получаем
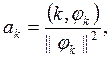
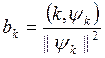
Здесь ![]() ,
, ![]() (см.,
(2.4)).
(см.,
(2.4)).
Тогда ряд Фурье по системе (Т1) имеет вид
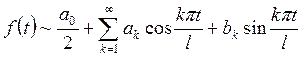 ,
(ФТ1)
,
(ФТ1)
где коэффициенты Фурье считаются по формулам
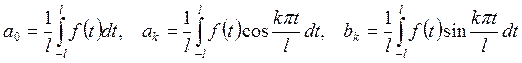 (КФТ1)
(КФТ1)
Сходимость ряда
(ФТ1) в среднем следует из теоремы 3.1. Спрашивается, каким условиям должна
удовлетворять периодическая функция ![]() периода
периода
![]() для того
что бы n-я частичная сумма
для того
что бы n-я частичная сумма ![]() ряда
(ФТ1) сходилась к
ряда
(ФТ1) сходилась к ![]() поточечно.
поточечно.
Определение. Будем
говорить, что функция ![]() удовлетворяет
условиям Дирихле на [a,b], если:
удовлетворяет
условиям Дирихле на [a,b], если:
а. Функция ![]() непрерывна
на [a,b], либо имеет конечное число точек
разрыва первого рода;
непрерывна
на [a,b], либо имеет конечное число точек
разрыва первого рода;
б. ![]() монотонна
на [a,b], либо имеет конечное число
экстремумов.
монотонна
на [a,b], либо имеет конечное число
экстремумов.
Теорема Дирихле.
Пусть ![]() периодическая
функция с периодом
периодическая
функция с периодом ![]() и
на каждом конечном отрезке
и
на каждом конечном отрезке ![]() удовлетворяет
условиям Дирихле. Тогда:
удовлетворяет
условиям Дирихле. Тогда:
1) Ряд Фурье (ФТ1) сходится в каждой точке t числовой оси;
2) Сумма ![]() ряда
Фурье (ФТ1) равна функции
ряда
Фурье (ФТ1) равна функции ![]() во
всех точках непрерывности функции
во
всех точках непрерывности функции ![]() ;
;
3) Сумма ![]() ряда
Фурье (ФТ1) равна
ряда
Фурье (ФТ1) равна
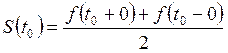
если ![]() - точка
разрыва первого рода для
- точка
разрыва первого рода для ![]() ,
где
,
где
![]()
Равенство Парсеваля для ряда (ФТ1) имеет вид
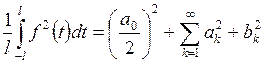
Пример. Разложить
в ряд Фурье периодическую функцию с периодом ![]() =2,
заданную следующим образом
=2,
заданную следующим образом
![]()
Решение. График заданной функции имеет вид
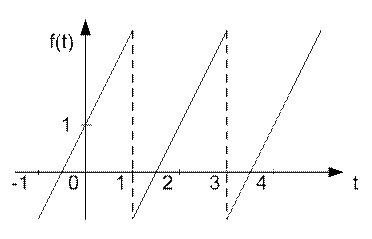
Рисунок 4.1
Данная функция
является непрерывной на [-1, 1]. Найдем коэффициенты Фурье функции ![]() по
формулам (КФТ1).
по
формулам (КФТ1).
Имеем
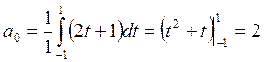
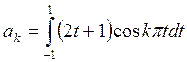
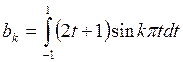
Интеграл вычислим по частям, полагая
![]()
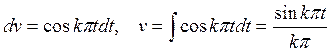
Тогда
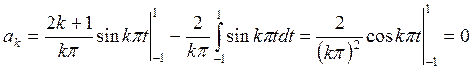
Аналогично
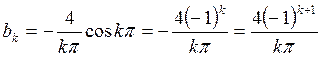
ряд заданной функции имеет вид
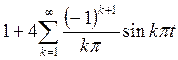
Согласно теореме Дирихле мы можем записать следующее равенство:
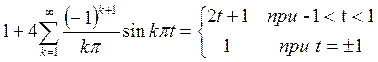
Равенство Парсеваля
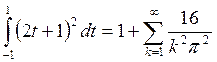
5 РЯД ФУРЬЕ ПО КОСИНУСАМ И СИНУСАМ ДЛЯ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ, ПЕРИОДА l ЗАДАННОЙ НА [0, l]
Пусть
периодическая функция ![]() периода
l на отрезке [0,l] является кусочно-непрерывной. В пункте
2 указано, что система функций (Т2)
периода
l на отрезке [0,l] является кусочно-непрерывной. В пункте
2 указано, что система функций (Т2)
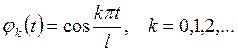 (Т2)
(Т2)
является полной ортогональной
системой функций на [0, l].
Тогда согласно теореме 3.1 для ![]() можно
построить ряд Фурье системе (Т2), который сходится к
можно
построить ряд Фурье системе (Т2), который сходится к ![]() в
среднем.
в
среднем.
Данный ряд имеет вид
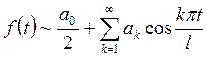 (ФТ2)
(ФТ2)
где коэффициенты Фурье, согласно формулы (КФ) пункта 3 находятся следующим образом:
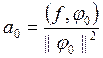 ,
, 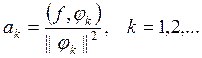
Так как 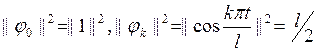 , то
последние соотношение преобразуется к виду
, то
последние соотношение преобразуется к виду
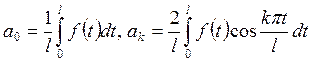 (КФТ2)
(КФТ2)
Равенство Парсеваля имеет вид:
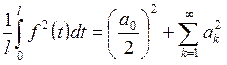
Если строить ряд Фурье по системе (Т3), то есть по системе синусов, то он будет иметь вид
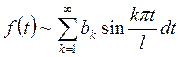 (ФТ3)
(ФТ3)
для которого коэффициенты Фурье находятся по формулам
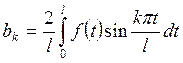 (КФТ3)
(КФТ3)
Равенство Парсеваля имеет вид
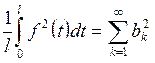
Задача 5.1. Предлагается сформулировать теорему Дирихле для рядов Фурье (ФТ») и (ФТ№).
При исследовании
суммы ![]() рядов
Фурье (ФТ2) и (ФТ3) остановим свой взгляд на точках 0 и l, где, вообще говоря, функция
рядов
Фурье (ФТ2) и (ФТ3) остановим свой взгляд на точках 0 и l, где, вообще говоря, функция ![]() на
является непрерывной. Оказывается, что
на
является непрерывной. Оказывается, что
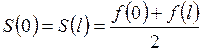
Аналогично,
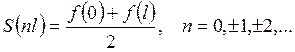
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.