Расчет частотных характеристик цепи. Сумма действительных членов полиномов соответственно числителя и знаменателя

4.3 Расчет частотных характеристик цепи

Как указывалось в разделе 4.1 переход от передаточной функции  к комплексному коэффициенту передачи  осуществляется заменой в выражении  переменной  на . Применяя этот прием к (4.4), получим:

,

(4.12)

где  и -сумма действительных членов полиномов соответственно числителя и знаменателя;

 и -сумма мнимых членов этих полиномов.

Очевидно:

(4.13)

Из (4.12) следует, что АЧХ определится выражением:

(4.14)

Физический смысл АЧХ – это зависимость модуля комплексного коэффициента передачи от частоты входного сигнала.

Выражение для расчета ФЧХ:

(4.15)

Для того, чтобы выяснить физический смысл ФЧХ, запишем  в показательной форме:

,

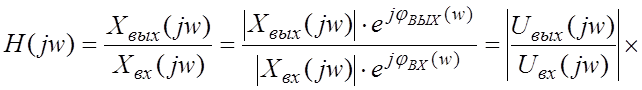
Отсюда следует, что ФЧХ цепи равна

и показывает, как от частоты зависит сдвиг фаз  между выходным и входным сигналом цепи.

Для построения характеристик  и  необходимо задаваться последовательностью значений частот  и при каждой из них по формулам (4.13)-(4.15) рассчитывать ординаты АЧХ и ФЧХ. Обычно при построении графиков АЧХ и ФЧХ используется либо равномерная шкала частот, при которой

, где -шаг изменения частоты, либо логарифмическая шкала частот, при которой очередное значение частоты определяется из соотношения:

Объединяя два этих выражения, можно записать

(4.16)

При этом, задаваясь , получаем равномерную шкалу, а при  - логарифмическую шкалу частот.

При расчете может быть неизвестен диапазон частот , в котором располагается область частотной характеристики. В этом случае рекомендуется, задав шкалу частот выбором коэффициентов  и , обозреть широкий диапазон при относительно небольшом числе рассчитываемых частот. Этот расчет используется лишь для уточнения диапазона частот, в котором следует строить искомые характеристики.

Пример 4.2. Используя выражение передаточной функции, полученное в примере 4.1, рассчитать частотные характеристики анализируемой цепи.

Воспользовавшись связью между  и  (4.3), получим:

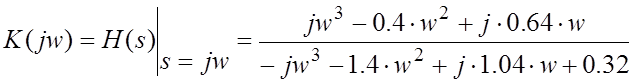
Откуда:

;

;

Зададимся коэффициентами  и , т.е. выберем логарифмическую шкалу частот, и значениям масштабированных частот  и .

Поскольку масштабный коэффициент для частоты , то это соответствует частотам

 и

По выражениям (4.14) и (4.15) найдем значения АЧХ и ФЧХ в выбранном диапазоне частот. Представим расчет в виде таблицы 4.1:

Таблица 4.1 – Результаты расчета АЧХ и ФЧХ цепи

,Гц
			0.127	0.46	0.989	0.999
, рад	1.569	1.55	1.4	0.28	0.156	0.001

Анализируя результаты вычислений , вычислений, можно сделать вывод, что в диапазоне частот от  до  изменения АЧХ практически не происходит, поэтому можно уточнить расчет характеристики в более узком диапазоне частот ( до ).

По значениям таблицы 4.1 построены графики АЧХ и ФЧХ (рисунок 1.5).

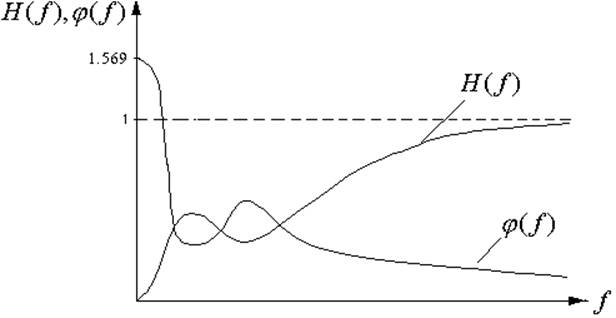
Рисунок 4.5 – Графики АЧХ и ФЧХ цепи

4.4 Расчет временных характеристик цепи

К временным характеристикам цепи относятся переходная  и импульсная  характеристики.

4.4.1 Расчет переходной характеристики

Переходная характеристика  есть отклик цепи на единичную функцию  при нулевых начальных условиях, поэтому будем считать, что  при .

Воспользуемся уравнением состояния (3.2) и уравнением выхода цепи (3.3); полагая, что , а . Получим систему уравнений

	(4.17)
	(4.18)

Здесь и далее для случая, когда на входе цепи действует  принято обозначение вектора состояния  вместо .

Для расчета переходной характеристики необходимо найти значение вектора состояния  путем интегрирования системы дифференциальных уравнений (4.17) и затем найденное значение вектора состояния  подставить в правую часть выражения (4.18).

Для системы дифференциальных линейных уравнений (4.17) известно решение:

(4.19)

Здесь  выражается через известное  ( есть  для момента времени ).

Входящая сюда экспоненциальная функция от матричного аргумента определяется выражением

(4.20)

Для сокращения записи обозначили  - шаг интегрирования.

Так как входящая в выражение (4.19) экспоненциальная функция выражается бесконечным рядом, то при практических расчетах пользуются её приближенным значением, удерживая конечное число первых членов ряда (4.20). Очевидно, такое приближение будет тем точнее, чем меньше шаг интегрирования . В связи с этим для обеспечения высокой точности расчета выбирают шаг интегрирования достаточно малым и выражением (4.19) пользуются как рекуррентным: по заданному значению  находят , далее найденное значение  подставляют в правую часть выражения и находят  и т.д.

В соответствии с таким приемом расчета выражение (4.19) можно представить в виде разностного уравнения:

,

(4.21)

где

(4.22)

В зависимости от числа удерживаемых в разложении экспоненциальной функции членов ряда можно строить методы интегрирования разного порядка:

метод первого порядка ():

; ;

метод второго порядка ():

;

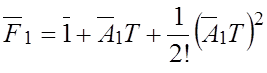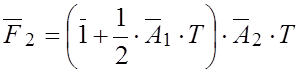
и т.д.

Формулы с таким способом определения коэффициентов  и  уравнения (4.21) будем называть явными формулами интегрирования.

Погрешность вычисления за счет приближенного представления  на одном шаге интегрирования пропорциональна . С уменьшением шага  эта погрешность уменьшается и тем значительнее