Структурная схема канала связи. Схемные решения AM модуляторов. Расчет статической модуляционной характеристики, страница 7

AM полоса частот Δω_0,7 = 2Ω_в, то при ОБП она вдвое уже!

2.3                      Преобразование частот

На выходе модулятора (умножителя) образуются частоты (ω₀ ± Ω), но если на оба входа умножителя подать только высокочастотные напряжения, то получим (ω₀ ± ω _г), где ω₀ – средняя частота сигнала, ω _г – частота гетеродина (маломощного местного генератора).

Тогда такой «умножитель» обычно называют смесителем, а вместе с гетеродином – преобразователем частоты. Обратим внимание, что при (ω ₀ + ω _г) – образуется еще более высокая частота, а при (ω ₀  – ω _г) – более низкая частота. Таким образом, поставив контур, настроенный на ту, или иную частоту получим преобразование вверх по частотному диапазону, либо вниз. Практически нет ни одного профессионального устройства связи, где бы ни использовались преобразователи частоты в нужную сторону. Сочетание ОБП с преобразователями вверх, позволяет создать МЭС с частотным уплотнением.

2.4                      Угловая (ФМ и ЧМ) модуляция

ФМ и ЧМ колебания вызывают изменения углового положения вектора несущей частоты, только при ФМ положение вектора прямо пропорционально амплитуде приложенного низкочастотного колебания, а при ЧМ – интегралу от него. Действительно, если ВЧ колебание S(t) = U_m cos[ω₀t + φ(t)], то при ФМ φ(t)= Δφ · cosΩt, где Δφ – индекс модуляции, обычно Δφ_mах = π; а при ЧМ: ω(t)= (ω_о + Δω · cosΩt), где Δω – девиация частоты (отклонение частоты от резонансной (ω₀)) под воздействием максимальной амплитуды информационного сообщения. При ЧМ Δω может быть любой, сколь угодно большой. Ограничивается только полосой пропускания приемника и передатчика. При ЧМ результирующее выражение для высокочастотного сигнала будет иметь вид:

S_чм (t) = U_m cos[ω₀t + ∫Δω cosΩtdt]

S_чм (t) = U_m cos[ω₀t + sinΩt](2.4)

В то же время

S_Фм (t) = U_m cos[ω₀t + Δ φ_max cos Ωt]                                                                                                                                                                     (2.5)

Видно, что с математической точки зрения оба колебания почти одинаковы, только индекс модуляции:

М =  =  – для ЧМ;

М = Δφ_тлх – для ФМ.

Рассмотрим подробнее выражение для ЧМ сигналов (2.4):

S_чм (t) = U_m cos[ω₀t + M sinΩt] = U_m cosω₀t · cosM sinΩt – U_m sin ω₀t · sinM sinΩt      (2.6)

Выражение (2.6) является довольно сложным, чтобы его упростить, можно положить М<<1, т.е. случай ЧМ с малой расстройкой, малым индексом модуляции. В принципе индекс частотной модуляции может принимать значения от 0 до ∞. Конечно, крайние значения нереальны, но по сравнению с AM при ЧМ возможен М>>1, что приведет к увеличению уровня полезной информации в ВЧ сигнале передатчика.

При M<<1 cosM sinΩt ≈ l, a sinM sinΩt ≈ MsinΩt. Тогда из (2.6) получим:

S_чм (t) = U_mcosω₀t · cosMsinΩt – U_m sin ω₀t · M sinΩt = U_m cosω₀t + U_m· cos(ω₀ + Ω)t – – U_m· cos(ω₀ – Ω)t

Выражение (2.7) свидетельствует, что спектр ЧМ колебаний при малых индексах модуляции равен спектру AM, только нижняя боковая частота находится в противофазе. Тогда спектр ЧМ колебаний может быть представлен графиком (рисунок 2.8).

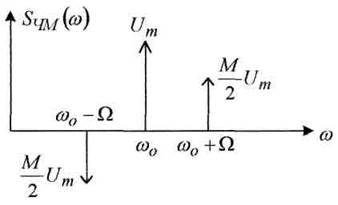
Рисунок 2.8.

Векторная   диаграмма   ЧМ   сигнала   при   малых   индексах   модуляции изображена на рисунке 2.9,а.

а)

б)

Рисунок 2.9.

В отличие от спектра AM разностная частотная составляющая направлена в противоположную сторону и, таким образом, суммы двух боковых частот при различных их амплитудах будут приводить к качанию вектора на некоторый угол Δφ) – произойдет частотная модуляция сигнала без изменения его амплитуды. На рисунке 2.96 – приведена схемная реализация ЧМ – модулятора.

В случае если М>1 решение уравнения (2.6) возможно лишь с помощью специальных функций Бесселя первого рода:

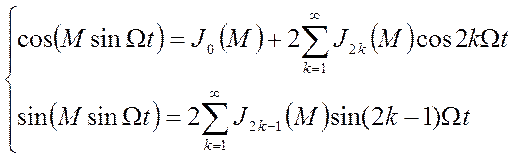
при этом, в зависимости от величины М, количество членов разложения по