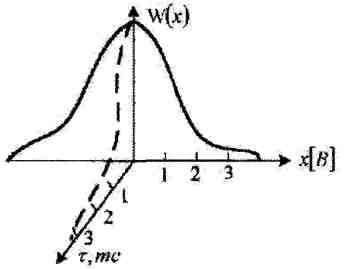
Рисунок 4.11 Случайные процессы, у которых W(x) = В(τ) – одинаковые степени взаимосвязи (убывания), носят название эргодических процессов. Стацио-нарные в широком смысле процессы ССП это у которых:
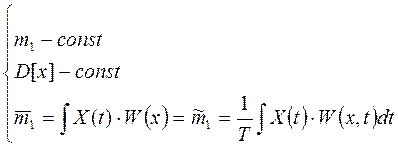
т.е. они эргодичны.
Какая зависимость W(x) или В(τ) является более важной для радиосвязи?
Конечно W(x), мы высокий уровень должны подать таким, чтобы он вышел за пределы нулевых значений, т.е. все что превысило «1» – высокий уровень должен надежно фиксироваться и малые помехи (вероятность которых велика!) не должны вызывать ложного срабатывания, (рисунок 4.12).
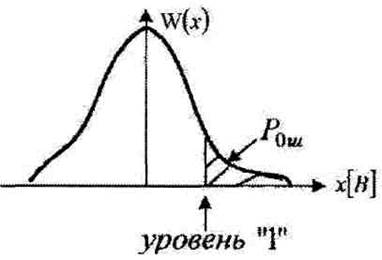
Рисунок 4.12
Повышать уровень единицы еще больше – нецелесообразно: все равно помехи простираются до + ∞ (только их все меньше и меньше!) но увеличение порогового уровня «1» в два раза потребует увеличения мощности передатчика в
четыре раза! А это: высокая стоимость, большие «помехи» соседям, экологически вредно (санитарная норма для человека не соблюдается!).
Вот почему вид функции W(x) в реальном канале связи (на приемном конце) должен быть надежно измерен. Рассчитать его очень трудно: множество случайных помех, самые причудливые затухания сигнала по трассе и т.п.
Но чтобы снять W(x) надо иметь множество приемных каналов (≈ 100 для ± 1% точности), которые бы в один момент времени одновременно давали измерения. Но ведь большинство случайных процессов стационарно и эргодично! Значит, вместо 100 приемников можно взять один и провести замеры через интересующие интервалы времени (длительность импульса) в 100 точках по времени! Полученная В(τ) ≈ W(x) и можно решать вопрос об оптимальном пороге.
Связь между функцией корреляции и спектром
случайного сигнала
ССП имеет время «жизни» равное τk но ведь длительность процесса определяет спектр. Аналогичные соотношения доказаны Винером-Хинчиным и выглядит следующим образом:
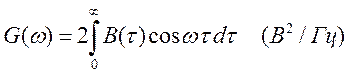(4.8)
здесь вместо 
взят cos (ωτ), т.к. В(τ)
— функция четная.
Обратная взаимосвязь позволяет получить В(τ) зная спектральную плотность по мощности:
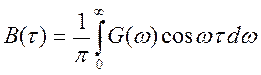(4.9)
Для определения мощности сигнала достаточно взять:
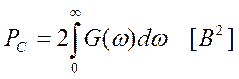(4.10)
Это уравнение Парсеваля для стационарных случайных процессов.
На основании вышеизложенного, становится необходимым создать прибор – коррелометр, который должен работать по алгоритму:
,
значит для электрического сигнала S(t) будем иметь:
(рисунок 4.13).
|
|
ЛЗ - линия задержки с n отводами через интервалы τ
|
|
|
- интергаторы |
- умножители
Рисунок 4.13
Таким образом, линия задержки и умножитель с интегрирующими цепочками позволяет построить анализатор случайных процессов, что аналогично параллельному спектроанализатору с п независимыми фильтрами и квадра-тичными детекторами для измерения мощности случайных процессов. Следует подчеркнуть, что сочетание ЛЗ, умножителя и интегратора – является типовым звеном для улучшения помехоустойчивости (автокорреляционный) прием.
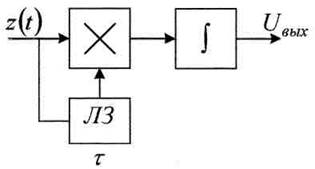
Рисунок 4.14
Здесь смесь сигнала и шума z(t) не сразу поступает на решающее устройство, а проверяется превышение уровня «0» (т.е. наличие»1») на
протяжении длительности τ. При наличии помех случайное превышение уровня «1» всегда возможно, но если оно сохраняется на всей длительности импульса –то это не случайная помеха, а точно – сигнал. Использование статистических числовых характеристик случайных сигналов позволяет значительно улучшить качество приема. Поэтому эти характеристики надо знать и правильно применять при приеме, т.к. в 100% случаев принятый сигнал – случайный.
С помощью коррелометра можно построить всю функцию В(τ), на практике часто пользуются понятием интервал корреляции
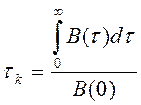(4.12)
определяемый как время в течение которого импульс отличен от нуля. τk может быть найден путем графического (приближенного) интегрирования, (рисунок
4.15).
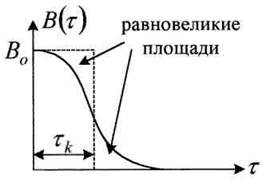
Рисунок 4.15
Точно также из графика G(ω) можно взять эффективную полосу пропускания:
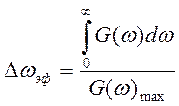
Между Δωэф и τk должна существовать определенная связь, выясним это опреде-лив произведение
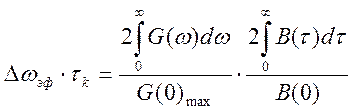(4.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
