Структурная схема канала связи. Схемные решения AM модуляторов. Расчет статической модуляционной характеристики, страница 15

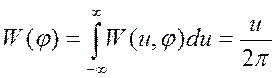
т.е. оно равновероятно и наличие шумов приводит к распределению вектора в виде окружности вокруг центрального значения с релеевским распределением амплитуд.  Таким образом,  если имеется вектор детерминированного сигнала и_т ↑ , то вокруг него «облако» шумов, в котором амплитуда в 50% случаев имеет величину σ (среднеквадратичного отклонения).

Рисунок 4.20

Причем, чем дальше от центра окружности, тем амплитуда все меньше. Зная W(u) и W(φ) можно рассчитать величину помехи по амплитуде и углу (ФМ).

В качестве примера рассмотрим построение В(τ) для прямоугольного видеоимпульса длительностью Т и радиоимпульса S(t) одинаковой длительности (рисунок 4.21).

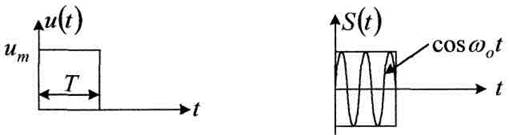
Рисунок 4.21

Имеем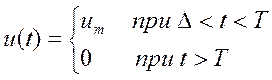  

и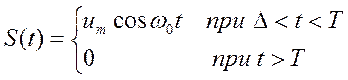        

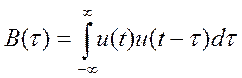– взаимная площадь прямоугольников, сдвинутых по t.

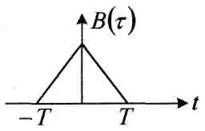
Рисунок 4.22

4.5 Прохождение случайных процессов через линейные и нелинейные цепи

Рассмотрим  случай  прохождения  ССП   x(t)  с  известной   w(x)   через линейный фильтр, имеющий характеристику .

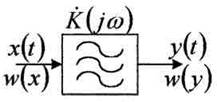
Рисунок 4.23 - Линейный фильтр

Задача состоит в определении y(t) и плотности вероятности w(y).

Наиболее просто можно найти энергетический спектр на выходе системы G_y(ω)  и связанной с ним функции корреляции В_y(τ). Амплитудный спектр S(ω) с использованием аппарата Фурье a 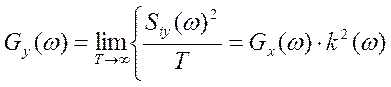 т.е. спектр на выходе фильтра есть его энергетический спектр на входе, умноженному на квадрат АЧХ фильтра без учета фазовой характеристики.

Корреляционная функция на выходе фильтра из (4.9)

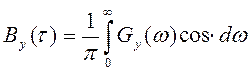
Следовательно, при воздействии ССП на линейную систему на выходе наблюдается  также  стационарный  случайный  процесс  с   G_v(ω)   и   В_у(ω), дисперсия которого .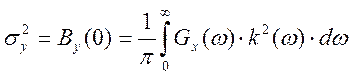

В качестве примера рассмотрим прохождение «белого» шума со спектральной плотностью N₀ В²/Гц [G_x(ω) = N₀ – const] через идеальный полосовой фильтр, характеристика которого:

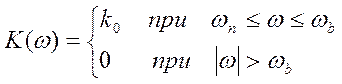
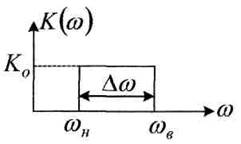
Рисунок 4.24

Тогда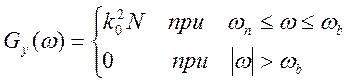

а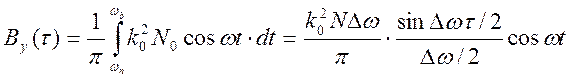

где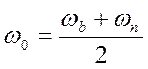

Рисунок 4.25

Закон распределения вероятностей ССП на выходе линейной инерционной системы отличается от W(X) и может быть определен, если ССП воздействует на узкополосную систему, тогда на выходе происходит процесс нормализации закона распределения. Т.е. W(Y) в этом случае определяется (4.10). Отсюда вывод: если W(X) – нормальный закон, то и W(Y) тоже нормальный, изменяется только G_y(ω) и В_у(ω), и соответственно σ.

При нелинейном преобразовании случайных процессов у = f(x) – какая-то нелинейная функция. При этом известно и ее обратная функция х = φ(у). Например, часто в технике связи для измерения мощности используется квадратичное детектирование, когда напряжение на выходе детектора у=х², тогда х = φ(у) состоит из двух корней .

Если рассматривать случайные величины х и у в достаточно малом интервале, то W(x)∙dx = W(y)∙dy

Откуда находим 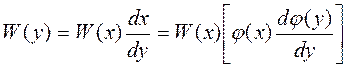 , а для числовых характеристик будем иметь: .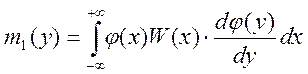

Для   случая  квадратичного   детектора  имеем   , 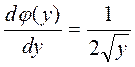;  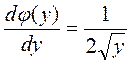тогда

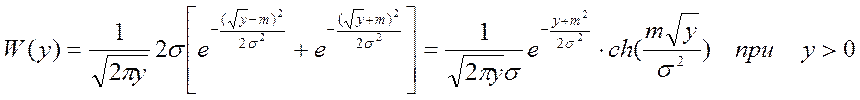
Для   нормального   случайного   процесса   с   нулевым   средним   (m=0) выражение упрощается: 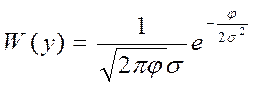распределение для квадратичного детектора.

График этого ССП приведен на рисунке:

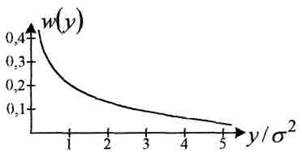
Рисунок 4.26

Если рассмотреть график гармонического колебания со случайной фазой

, где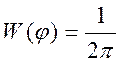

То обратная функция 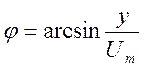; Производная от обратной функции:

.

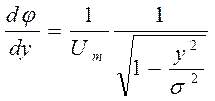Получим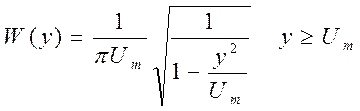

График распределения плотности синусоидального процесса:

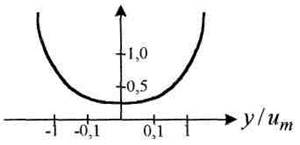
Рисунок 4.27

Синусоида имеет плоскую вершину и вероятность присутствия неболь-шого приращения Δk: вблизи U_т имеет максимум. При y>U_m  ничего нет, это детерминированный сигнал. Нетрудно сообразить, что W(Z) – смесь «белого» шума и амплитуды дает распределение; рисунок 4.28. По наличию смены производной можно определить Uш, выделить сигнал из смеси с/ш.

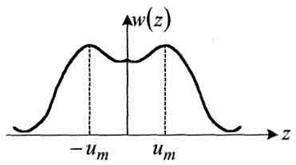
Рисунок 4.28