(двукратных изменениях частоты) а радиоинженеры – более широко в гармониках (первая, вторая – десятая, двадцатая и т.д.). Если привести спектр Сk для электрических сигналов, то он всегда падающий, (рисунок 4.3).
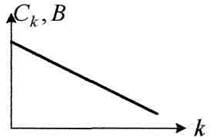
Рисунок 4.3.
Если энергия сигнала величина постоянная, то с ростом частоты ее амплитуда уменьшается т.к. ε = hf 2 – закон Планка.
Наглядное представление периодического сигнала в виде набора гармоник приведено на рисунке 4.4.
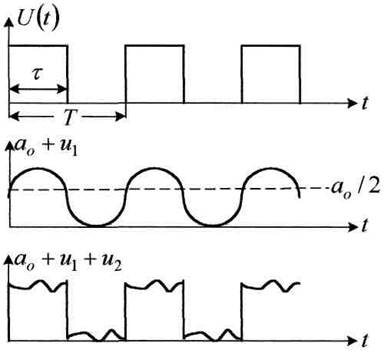
Рисунок 4.4
Где а0 + u1 – график из первой и средней амплитуды. Видно, что (а0 + u1) повторяет качественно картинку: положительные и нулевые значения совпадают. (а0 + и1 + и2) – более точно описывает импульсную последовательность и только если число синусоид продлить до ∞, то получим чисто прямоугольный импульс.
Эту периодическую последовательность (4.1) можно записать в виде:
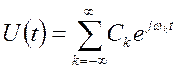
(4.2)
Где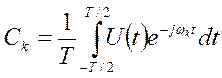 
.
4.2 Непериодические сигналы
Воспользовавшись преобразованием
Эйлера, выражение (4.2) невыпол-нимо,
т.к.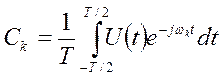 
при Т → ∞ обращается в нуль. Поэтому, когда сигнал не повторяется (Т
→ ∞), то вводят новую величину – спектральную плотность сигнала S(ω) = Ck · T – имеющую размерность В/Гц, и показывающую распределение амплитуд на каждый Герц полосы.
При этом (4.2) модифицируется в интеграл Фурье
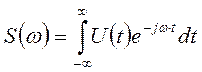(4.3)
чтобы лучше понять эти преобразования найдем спектральное представление одиночного импульса, имеющего длительность τ (рисунок 4.5).
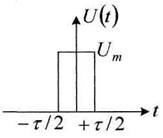
Рисунок 4.5
Для упрощения
представим, что импульс четный (симметричный) относительно оси «у». Тогда в спектре (4.3) будут
присутствовать одни четные (cos) функции: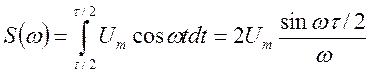 
,
умножим числитель и знаменатель
на τ/2 и окончательно
получим:
,
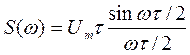(4.4)
где Umτ – площадь импульса;
–
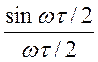затухающая синусоида при τ = 0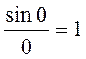 
– первый замеча-тельный предел. Эта величина обратится в нуль,
когда ωτ / 2 = π(числитель равен «0»), т.е.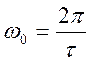 
и
этот минимум будет повторяться в точках:
2ω0, 3ω0 и т.д.
Тогда график спектральной плотности одиночного импульса имеет вид:
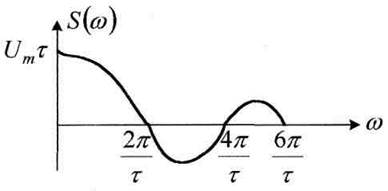
Рисунок 4.6
Амплитуды каждого лепестка
будут уменьшаться в 
раз
(2ой – в два раза меньше, 3ий – в три и т.д.). Поэтому
основной лепесток спектра простирается от 0 до 2π/τ, ΔF = 
(Гц), таким образом, спектр импульса
обратно пропорционален его
длительности, чем уже импульс, тем шире спектр. При т → ∞ (постоянный ток) спектр равен «0» (рисунок 4.7а), а при τ → 0 (δ – функция) спектр равномерен в широком диапазоне частот (рисунок 4.7б).
|
|
а)
б)
Рисунок 4.7
Вот почему очень короткие импульсы (в виде δ – функции) используются для снятия характеристик усилителей: они захватывают все частоты.
Если же говорить о мощности детерминированных сигналов, то она равна
квадрату амплитуды (поделенная на 1 Ом), т.е. для периодических сигналов
–
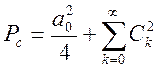равенство Парсеваля (4.5)
т.е. мощность определяется мощностью постоянного тока плюс мощность всех гармонических составляющих без учета фазовых сдвигов, т.к.
(cos2 ωkt + sin2 ωkt) ≡ 1.
В случае непериодических сигналов
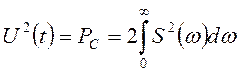(4.6)
равенство Парсеваля для непериодических сигналов.
Если в (4.4) подставить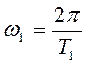 
и
т.д., то получим спектральную плотность
периодической последовательности импульсных сигналов.
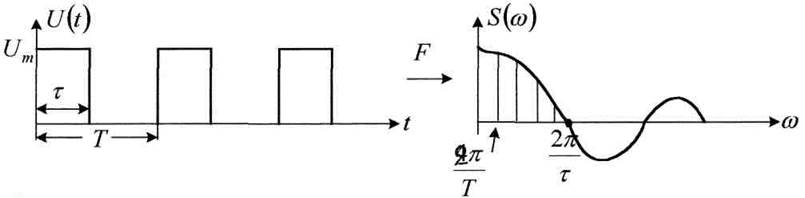
Рисунок 4.8
Спектр импульсной последовательности, в
отличие от спектра одиночного импульса, дискретный и состоит из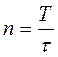 
гармоник,
но ширина основного лепестка по прежнему 
.
Следует отметить, что U(t) и S(ω) связаны прямым и обратным преобразованием Фурье:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
