В модуляторе на выходе управляемого b(kAt) триггера выходят сигналы или «0» или «1», сдвинутые друг от друга на 180° (π). Для обеспечения нормальной работы ФМ демодулятора требуется наличие когерентного напряжения от Гв/ч (опорная фаза). Путем перемножения КГ с z(t) в зависимости от того, какой сигнал присутствует в z(t) на выходе демодулятора возникают сигналы «+1» или «-1».
Более подробно схемы и принципы работы модуляторов и демодуляторов различных видов изложены в разделе 2.
Рассмотрев структурную схему канала связи, и прохождение сигнала от источника к получателю отметим, что для инженера связи необходимо выполнить оптимальные (наилучшие) условия передачи информации. Но эта оптимальность может быть рассмотрена с точки зрения: наилучшего кодирования сигналов, с целью повышения скорости передачи, ее автоматизации; наибольшей помехоустойчивости
(как можно большему обеспечению отношения h2); наибольшей верности распознавания сигналов (минимум вероятности ошибок) и т.п. При этом в ТЭС не рассматривают улучшение этих параметров за счет увеличения мощности передатчика, а за счет оптимальной обработки в приемном устройстве (уменьшения уровня помех). Увеличение мощности передатчика приводит к:
1. Резкому увеличению затрат на сооружение и эксплуатацию.
2. Увеличению помех для соседних станций (операторов).
3. Не безопасно с экологической точки зрения.
В то же время, непримерное наличие помех и случайных сигналов на входе приемника требует довольно сложных (нелинейных) методов обработки сигналов. Решение этой задачи, созданию оптимального алгоритма, а по алгоритму и построение оптимальной функциональной схемы канала связи – основная проблема курса.
В настоящее время, благодаря развитию интегральной технологии, появилась возможность создавать схемотехнические решения канала в виде готовых функциональных элементов, что позволяет осуществлять любые сложные преобразования сигналов.
2 МОДУЛЯЩЯ СИГНАЛОВ
2.1 Амплитудная модуляция
AM – самый простой и самый первый способ переноса полезной
(низкочастотной) информации с помощью электромагнитных колебаний высокой частоты. Если генератор излучает S(t)= Umcosω0 t, то для того, чтобы осуществить AM хотя бы одной частоты Ω необходимо выполнить условие SАM(t)= (Um + kАМUΩ · ·cosΩt)cosω0t. Т.е. величина огибающей ВЧ сигналапериодически меняется с частотой Ω и эта сумма должна быть умножена на cosω0t значит, с точки зрения схемотехники, амплитудный модулятор это умножитель на один вход которого поступает полезная НЧ информация, а на другой – непрерывный ВЧ сигнал (cosω0t). Это выражение обычно записывают
SAM (t) = Um (1 + mcosΩt)cosω0t, (2.1)
где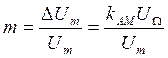 
–
коэффициент модуляции, может принимать значения от 0 до 1;
kAM – коэффициент передачи модулятора.
График AM колебания приведен на рисунке 2.1.
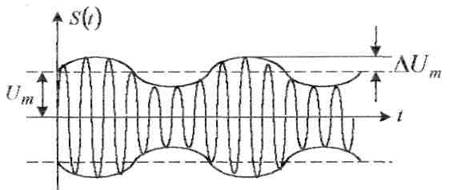
Рисунок 2.1
Если т= 1, то провалы в графике достигают оси ординат, а максимальное значение – 2Um . В случае т = 0 (UΩ = 0) график вырождается в косинусоиду с постоянной амплитудой Vт .
Воспользовавшись известным тригонометрическим выражением cos α · ·cos β = сos(α + β)+ cos(α – β), получим:
SAM(t)= Umcosω0t
+ 
Um(ω0
+ Ω)t + Um(ω0
– Ω)t (2.2)
откуда видно, что AM сигнал состоит из несущей частоты (ω0) и двух боковых (ω0 + Ω) и (ω0 + Ω).
Зависимость амплитуды AM сигнала от частоты (спектр AM сигнала) может быть представлен в виде: рисунок 2.2.
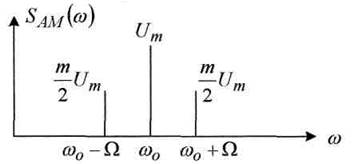
Рисунок 2.2
В реальных
телефонных каналах человеческий голос содержит не одну частоту, а целый набор циклических частот FTJIФ = (0,3
3,4)кГц изменяющихся по треугольному закону,
тогда реальный спектр AM ТЛФ, (рисунок 2.3).
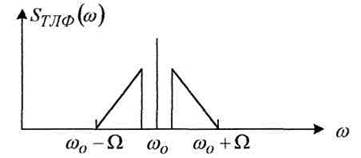
Рисунок 2.3.
Если построить векторную диаграмму AM колебания (2.2), то получим:
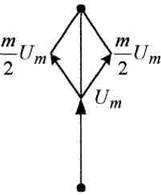
Рисунок 2.4 – Векторная диаграмма AM колебания
Где Um – вектор,
вращающийся с частотой ω0 и два вектора Um один опережающий вектор Uт на угол (ω0
+ Ω) и другой – отстающий на тот же угол. Т.к. частота Ω изменяет положение боковых лепестков, то они суммируются с основным
вектором, то вычитываются, благодаря чему и появляется AM
сигнал.
Если определить мощность сигнала на один ОМ то получим, возводя в квадрат выражение (2.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.