но
из (4.8) при ω
= 0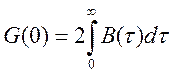 
, а из (4.9) при τ =
0 
.
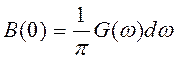Подставив их в (4.13) окончательно
получим 
или
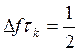. Если время «жизни» случайного выброса равно τk
, то при этом его спектр будет равен
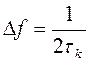(4.14)
и наоборот, зная полосу можно определить время корреляции случайного процесса.
4.4 Основные вероятностные характеристики случайных процессов в технике связи
В теории случайных сигналов фундаментальное значение имеет гауссово (или нормальное) распределение плотности вероятности
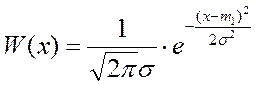(4.15)
Если т1 = 0, такой процесс называется центрированным, это распределение шумов.
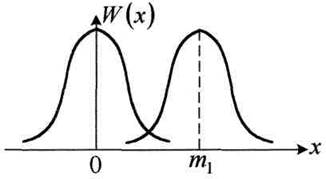
Рисунок 4.16 – Распределение шумов
По предельной теореме теории вероятностей при большом числе независимых событий с любыми законами распределения, суммарный закон стремится к нормальному. В технике связи влияющих факторов, помех великое множество и в отсутствии сигнала это центрированный процесс: т.е. выбросы в
отрицательном и положительном направлении равновероятны и убывают по экспоненциальному закону (большие положительные выбросы очень редки, также как и отрицательные), (рисунок 4.16).
Рисунок 4.16
Вероятность превышения сигнала уровня 2В равна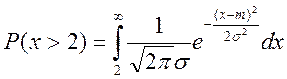 
т.е. равна площади кривой W(x) от 2 до ∞,
а Р(-∞ < х < ∞)
= 
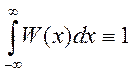
Если определить функцию распределения вероятностей для центрированного процесса, то она будет иметь вид: F(x) = ∫W(x)dx и в точке
х = 0 F(x)=0,5.
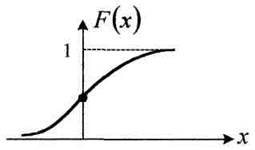
Рисунок 4.17
Широкополосные и узкополосные процессы
Если энергетический спектр случайного процесса сосредоточен вокруг центральной частоты ω0 , причем Δωэф << ω0 – такой процесс называется узкополосным, (рисунок 4.18).
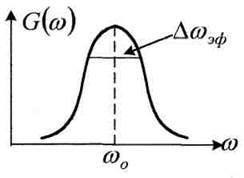
Рисунок 4.18
Такой спектр имеют помехи на выходе избирательного контура (например, на
выходе УПЧ).
Широкополосным процессом будет такой как на рисунке 4.6б, при этом сигнал будет иметь вид δ – функции, у которого τk = 0. По аналогии с белым светом, который состоит из множества отдельных цветных полос (различных частот), случайный процесс с τk ≈ 0 носит название «белого» шума. На самом деле бесконечно равномерного спектра в природе не существует (также как τ = 0), но тепловые флуктуации электронов, масса которых ничтожно мала, имеют равномерный спектр вплоть до мягкого рентгеновского излучения, поэтому в реальных условиях техники связи тепловые шумы считают «белым» шумом.
Если же говорить об узкополосных сигналах (рисунок 4.18), то их можно представить в виде двух ортогональных случайных процессов: u1(t) = U1 cosω0 t и u2(t) = U2 sinω0 t, т.е. u1 совпадает с вектором ВЧ сигнала на частоте ω0, а другой направлен под углом π/2.
Если оба сигнала нормальны и не коррелированны, то можно записать:
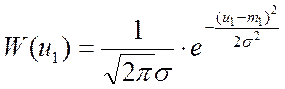и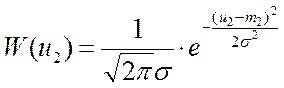 
Нас должен
интересовать модуль результирующего напряжения 
и его фазовый угол φ в полярных координатах: u1 = u ∙ cosφ и u2 = = u ∙ sinφ. Рассмотрение этого случайного сигнала в полярных
координатах нужно для того, чтобы получать закон
распределения амплитуд W(u)
и распределение по углу W(φ).
Первое распределение необходимо при оценке шумов в системах с амплитудной модуляцией, а второе – для угловых.
Перемножив W(u1) на W(u2), и выразив напряжения в полярных координатах, получим:
,
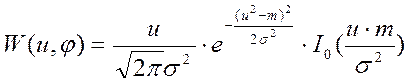(4.11)
где т – математическое ожидание при т1 = тг;
I0 – функция Бесселя нулевого порядка (табулирована).
Выражение (4.11) носит название обобщенного распределения Релея.
Если шум – центрированный процесс с т = т1 = т2 = 0, то I0 (0) = 1 и взяв интеграл по всем φ, получим распределение амплитуд по закону Релея
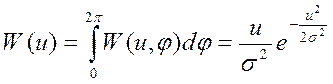(4.12)
по этому закону подчиняется распределение амплитуд на выходе УПЧ, на выход детектора, рисунок 4.19.
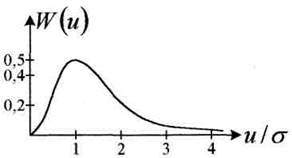
Рисунок 4.19
Распределение случайного процесса по углу:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.