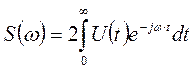Структурная схема канала связи. Схемные решения AM модуляторов. Расчет статической модуляционной характеристики, страница 12

– прямое                         (4.7)

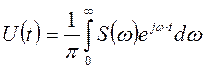 – обратное

Вид Uyt) определяет спектр, но по спектру можно восстановить сигнал. Поэтому в радиосвязи распространены методы спектрального анализа сигналов с помощью соответствующих приборов - спектроанализаторов (СА).

4.3 Случайные сигналы

Этот тип сигналов является наиболее общим и чаще всего отмечаемый на практике. Если представить себе суперпозицию (сложение) всех видов сигналов, присутствующих на входе приемного устройства, то она состоит из бесконечного множества различных электрических сигналов самого различного происхождения: полезной случайной информации, помех от множества источников, сигналов соседних станций, тепловых флуктуации носителей электричества и т.п. Все эти процессы образуют полный ансамбль событий, и каждый характеризуется плотностью вероятности [W(х,t)] или интегральным законом – функцией распределения вероятностей – F(x,t). При этом следует отметить, что они зависят как от уровня наблюдения по амплитуде, так и по времени.

Рисунок 4.9

Чтобы иметь общее представление о вероятности X – надо взять п – мерное распределение вероятностей отдельных событий (где п → ∞). Задача была бы невыполнимой, если бы на помощь не пришли методы статистической оценки события по некоторым числовым характеристикам:

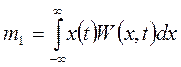– первый  момент,  или  математическое  ожидание. Наиболее достоверное значение амплитуды сигнала в «В» (среднее значение сигнала) за длительное время наблюдения.

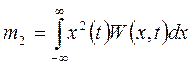 – второй момент случайного процесса (разброс мощ-ности) при этом выделяют дисперсию события.

D[x] = (m₂ – m₁²) – характеризующую разброс по мощности вокруг среднего значения. D[x] – имеет размерность В² для электрических сигналов и определяет мощность переменного тока (шумов) вокруг среднего значения.

 – называется среднеквадратическим отклонением сигнала от m₁.

Путем накопления множества измерений (статистической обработки) выяснено, что в большинстве случайных процессов эти величины сохраняют свои значения, такие процессы носят названия стационарных случайных процессов –ССП. Для ССП характерно: m₁ – const, D[x] – const. Т.е. уровень сигнала колеблется, но его среднее значение т₁ остается неизменным, а разброс D[x] – уровень помех, также сохраняется постоянным. Для электрических сигналов помехи в течение 1-2 секунд, пока мы распознаем сигнал, не меняются!

Утром помехи отличаются от дневных, когда интенсивность работы любых электроустановок возрастает, но ведь сообщение мы обрабатываем очень быстро! А уж распознавание соседних сигналов 0 и 1 вообще происходит за микросекунды! Вот почему сумма полезной информации и помех за небольшой отрезок времени выглядит:

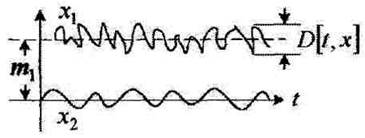
Рисунок 4.10

При этом событие с m₁ = 0 (x₂) меняется более медленно, чтобы опи-сать случайное событие достаточно точно надо знать его:

1.  математическое ожидание – m₁;

2.  дисперсию (т₂ – m₁²) – D[x];

3.  функцию корреляции – степень статистической взаимосвязи процесса  разнесенных во времени В(τ), при этом B(τ) = ∫x(t)∙x(t– τ)dτ – автокорреляционная функция. Характеризует как быстро во времени меняется процесс. На рисунке 4.10 процесс x₂ имеет больший интервал корреляции 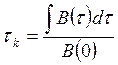, где В(0) – ищется при τ = 0. Функция корреляции обладает такими свойствами:

1.  В(0) – max;

2.  В(- 1)=В(+1) – функция симметричная (четная);

3.  усреднение по времени любых моментов равно усреднению по ан-самблю.

При этом время, в течении которого функция корреляции меняется от max до min(0) носит название интервал корреляции и характеризует среднюю длительность случайного процесса. Таким образом, можно описать зависимость случайной величины от амплитуды W(x) и от времени В(τ).

Например, на рисунке 4.10 от изменения амплитуды [В] функция меняет-ся так, что при х > 3В она исчезает, а во времени – при τ > 3, аналогично.