сообщение – тем больше несет оно информации. Если лектор 1 час будет повторять фразу: «дважды-два четыре», то информация не будет поступать студентам. Ее вероятность близка к 1 (все это знают!).
Но сообщения никогда не передаются одним символом (одной буквой), а используется целый ансамбль (алфавит) сообщений.
Значит надо суммировать отдельные символы в вероятностном плане, для этого используются логарифмические единицы, которые переводят произведение вероятностей в сумму, а так как основным кодовым символом в технике связи служат бинарные сигналы, то взят log по основанию 2. Таким образом, количество информации:
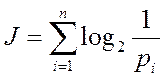[Бит] (5.1)
эта единица получила наименование Бит. Есть и более крупные единицы – Байт =
23 Бит.
Формирование сообщения – вероятностный процесс, тогда математическое ожидание его:
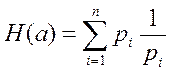[Бит/символ] (5.2)
носит название энтропии сообщения и характеризует количество информации, передаваемое одним символом. Для увеличения объема передаваемой информации надо добиваться, чтобы энтропия источника сообщения была максимальна.
Чтобы лучше понять эту физическую величину рассмотрим простейшее сообщение из двух символов (0 и 1).
При этом р(0) = 1 – р(1),
p(0) – вероятность появления символа «0»;
p(1) – вероятность «1».
Тогда энтропия такого сообщения:
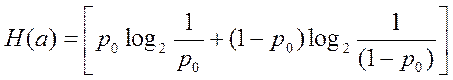
Построим график Н(а) = f [p(0)]
|
|
Рисунок 5.5
Если
p(0)=0, то первый член = 0, также как и второй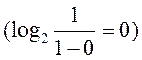 
.
Тоже самое произойдет и при p(0)=l. Энтропия равна нулю (информация не будет передаваться)
если стучать один (0 или 1). Энтропия максимальна, когда оба символа участвуют
в передаче 
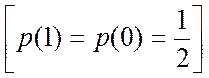и при бинарном сигнале m=2 передаётся как видно
из графика, максимум один бит информации.
Вообще, при любом числе импульсов сообщения, оптимальна
вероятность каждого символа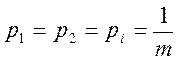 
и
при этом:
(5.4)
Если длительность посылки импульса Т, то производительность источника сообщения.
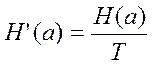(Бод)
(5.5)
Максимальная энтропия сообщения достигается при равновероятностных появлениях символов.
Но в любом языке вероятность присутствия букв неравновероятна. Например p(a) ≠ p(щ). Буква щ очень редко встречается. Чтобы исправить это положение прибегают к статистическому (экономичному) кодированию. Вначале для нужного языка в стандартном тексте, допустим, из 1000 букв подсчитывают число наличия буквы «а», затем «б», и т.д. И затем прибегают к неравномерному кодированию, в котором длительность символа в коде обратно пропорциональна
его вероятности: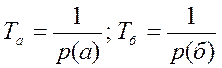 
и
т.д. Таким образом, самым коротким во времени символом кодируется наиболее часто встречающаяся буква и
наоборот.
Такой статистический код впервые был предложен Морзе в 1886 г., где точкой закодирована самая часто встречающаяся буква английского алфавита (е), а наборами тире и точек – менее вероятные буквы.
Неравномерный код (Морзе) статистически уплотнен, но трудно поддается автоматизации из-за неравенства во времени каждой буквы. Этот недостаток был устранен в 5-значном равномерном коде Бодо, где каждой букве алфавита соответствует комбинация из 5 бинарных символов, при этом число перестановок из 5 по 2 составило 25 = 32, что достаточно для обозначения всего латинского алфавита.
Смысловая матрица кода Бодо:
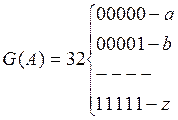
Теперь каждая строка (буква) занимает одинаковый интервал времени и легко передается (и принимается) с помощью телеграфного (буквопечатающего) аппарата. Дальнейшее улучшение равномерных кодов было направлено на их лучшую организацию и создание избыточных, корректирующих (исправляющих) кодов, которые рассматриваются во 2ой части курса ТЭС.
ЛИТЕРАТУРА
1. Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи – М: Радио и Связь, 1998, 432 стр.
2. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов – М: Радио и связь, 1996, 302 стр.
3. Баскаков С.И. Радиотехнические цепи и сигналы – М: Высшая школа,
1988, 448 стр.
4. Кловский Д.Д. Теория передачи сигналов – М.: Связь, 1979, 386 стр.
5. Зюко А.Г. Основы передачи сигналов – Одесса: ОИС, 1967, 282 стр.
6. Дмитриев В.И. Прикладная теория информатики – М.: Высшая школа,
1989, 320 стр.
7. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах – М:
Связь, 1978,351 стр.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
