Федеральное агентство связи
Хабаровский институт инфокоммуникаций (филиал)
ГОУ ВПО «Сибирский государственный университет
телекоммуникаций и информатики»
КУРСОВОЙ ПРОЕКТ
по дисциплине:
Математические основы цифровой обработки сигналов
на тему:
Расчет рекурсивного цифрового фильтра
Выполнил:
Проверил:
Шифр: 08013 ХР
2009 г
СОДЕРЖАНИЕ
|
Стр. |
|
|
Введение |
4 |
|
1. Требования к частотным характеристикам проектируемого фильтра |
5 |
|
2. Методы проектирования рекурсивных фильтров |
7 |
|
2.1. Метод инвариантности импульсных характеристик |
7 |
|
2.2. Метод инвариантности частотных характеристик (метод билинейного преобразования) |
8 |
|
3. Расчет передаточной функции аналогового фильтра-прототипа |
10 |
|
3.1. Проверка правильности расчета передаточной функции аналогового фильтра-прототипа |
10 |
|
4. Расчет передаточной функции проектируемого фильтра методом билинейного преобразования |
13 |
|
5. Расчет АЧХ проектируемого рекурсивного ЦФ |
14 |
|
6. Разработка структурной схемы рекурсивного ЦФ |
17 |
|
7. Принципы реализации ЦФ |
18 |
|
Заключение |
20 |
|
Список используемой литературы |
21 |
Введение
В настоящее время все более широкое применение в различных областях техники (в системах связи, радиолокации, гидролокации, геофизике, при обработке речевых сигналов, изображений и др.) находит цифровая обработка сигналов, имеющая ряд преимуществ (программируемость, повышенная точность, стабильность и др.) по сравнению с аналоговыми.
Уникальным свойством ЦФ является практически неограниченная память, позволяющая на низких частотах почти от нуля до единиц килогерц реализовать узкополосные фильтры с добротностью 103-104 и полосовые фильтры с переходной полосой 0,1 – 1 Гц. Это лучше того, что могут обеспечивать RC-, ПЗС- и кварцевые фильтры в том же диапазоне частот. Неограниченная память ЦФ дает возможность использовать широко применяемой в устройствах цифровой обработки сигналов режим работы с предварительным накоплением информации, который состоит в следующем: выборка входного сигнала в реальном масштабе времени со скоростью, определяемой возможностями аналого-цифрового преобразования, записывается в буферное ЗУ, затем с меньшей скоростью обрабатывается по заданному алгоритму. При этом могут быть обеспечены хорошие массогабаритные характеристики при обработке достаточно высокочастотных и широкополосных входных сигналов.
Широкое внедрение цифровой обработки в практические разработки и распространение ее в область высоких частот определяется, прежде всего, развитием интегральной технологии, повышением плотности упаковки и быстродействия, снижением потребляемой мощности БИС. Следует отметить, что возможности интегральной технологии далеко не исчерпаны. Быстродействие и потребляемая мощность современных ИС на 2-3 порядка не доведены до пределов, задаваемых возможностями технологии, еще 2-3 порядка может дать разработка и внедрение технологии цифровых схем на сверхпроводящих элементах.
1. Требования к частотным характеристикам проектируемого фильтра
Как правило, при проектировании частотно-избирательных ЦФ задаются требования к АЧХ и ФЧХ фильтров.
Требования к АЧХ. Дискретная цепь может осуществлять любые операции: частотную фильтрацию сигналов, корректирование характеристик, дифференцирование сигнала и т.д., т.е. выполнять функции любой аналоговой цепи. При проектировании частотно-избирательных фильтров требования задаются к АЧХ фильтров.
Так для идеального фильтра частот АЧХ имеет вид, приведенный на рисунке 1.1
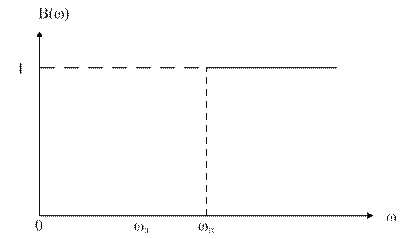
Рисунок 1.1 – АЧХ идеального ФВЧ
Очевидно, что невозможно реализовать дискретный фильтр, АЧХ которого точно равна функции В(ω). Поэтому необходимо аппроксимировать заданную функцию В(ω), т.е. определить параметры дискретного фильтра, АЧХ которого Н(ω) в том или ином смысле была бы близка к заданной (рисунок 1.2).
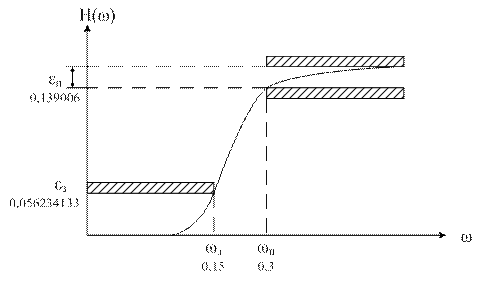
Рисунок 1.2 – Требования к АЧХ ФВЧ.
Н(ω) ≈ В(ω) при 0 ≤ ω ≤ ωн и ωз ≤ ω ≤ 0,5,здесь εн и εз – допустимые неравномерности АЧХ в полосе пропускания и в полосе задерживания соответственно; ωн и ωз – нормированные граничные частоты полосы пропускания и полосы задерживания фильтра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.