Расчет рекурсивного цифрового фильтра. Проверка правильности расчета передаточной функции аналогового фильтра-прототипа, страница 3

Использование подстановки обеспечивает преобразование передаточной функции H(s) аналогового фильтра-прототипа в передаточную функцию H(z) цифрового фильтра:

Однако соотношение между нормированными «аналоговыми частотами» Ω и нормированными «цифровыми частотами» ω является нелинейными.

Подставляя в выражение 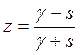, вместо z = e^j2πω и s = jΩ получаем:

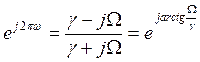
         Отсюда:

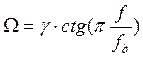
При изменении частоты f от 0 до 0,5f или ω от 0 до 0,5 нормированная частота Ω в шкале аналоговых частот будет пробегать значения от 0 до бесконечности. Таким образом имеет место «деформация» шкалы частот. На рисунке 2.2.1 показана трансформация частотной оси при билинейном Z-преобразовании для ФВЧ.

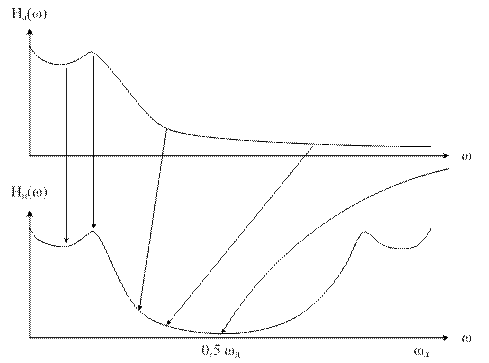
Рисунок 2.2.1 – Трансформация частотной оси при билинейном Z-преобразовании

Выход, однако, чрезвычайно прост. Деформация шкалы частот не приводит к нарушению избирательных свойств при билинейном преобразовании (и это главное). А деформация шкалы частот можно скомпенсировать с помощью предискажений в аналоговом фильтре. Компенсация эффекта деформации может осуществляться путем предварительного искажения шкалы частот аналогового фильтра противоположным образом, так, чтобы после применения билинейного Z-преобразования критические частоты были сдвинуты назад, к требуемым значениям.

3. Расчет передаточной функции аналогового фильтра-прототипа

Для расчета передаточной функции аналогового фильтра-прототипа необходимо рассчитать: нормированные «цифровые» частот ω_з и ω_п:

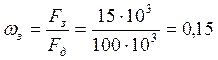
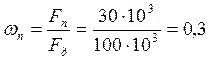
где ω_з – нормированная частота полосы задержки

ω_п – нормированная частота полосы пропускания

Из таблицы 5.1 (1) для ФВЧ находим:

где γ – постоянный множитель, не меняющий форму преобразования

где Ω_k – граничная «аналоговая» частота.

3.1. Проверка правильности расчета передаточной функции аналогового фильтра-прототипа

Рассчитаем допустимые неравномерности в полосе пропускания и задерживания по формулам:

По таблице А1 приложения А(1) определяем модуль коэффициента отражения |p|, для ΔА_max = 1,3 дБ, |p| = 50%. По номограмме А1.1 (1) находим вспомогательный параметр L, учитывая, |p| = 50% A_min = 25 дБ, L = 0,26.

По номограмме А2 (1) определяем порядок n передаточной функции H(s), учитывая L = 0,26 и Ω_k = 2,701301616.

Проверим фильтр 3го порядка.

В общем виде передаточная функция фильтра третьего порядка:

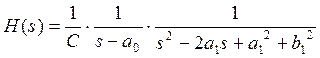
где C, a_i и b_i – коэффициенты, которые находим по таблице А2 приложения А (1):

Для фильтра Баттерворта 3го порядка:

С = 0,57735027

-a₀ = 1,2009369490

-a₁ = 0,6004684745

±b₁ = 1,0400419062

Таким образом, передаточная функция имеет вид:

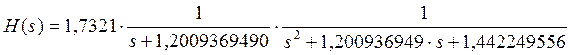
Для проверки, удовлетворяет ли фильтр 3го порядка заданным значениям рассчитываемого фильтра, необходимо проверить, выполняются ли условия:

H(1) ≥ 1 – ε_п и H(Ω_k) ≤ ε_з                                                  (1.1)

Для этого необходимо сделать замену переменных:

|H(jΩ)| = H(s)|_s = jΩ

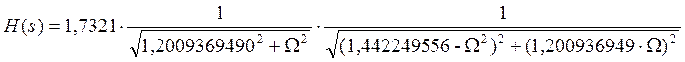
Подставляя вместо Ω:

При Ω = 0 получаем H(0) = 1

При Ω = 1 получаем H(1) = 0,86605 > 1 – ε_п = 0,861

При Ω = Ω_k = 2,701301616 получаем Н(Ω_k) = 0,087535363 > ε_з = 0,056234133

Убеждаемся, что фильтр 3го порядка не удовлетворяет заданным значениям рассчитываемого фильтра.

Проверим фильтр 4го порядка.

В общем виде передаточная функция фильтра из двух звеньев второго порядка:

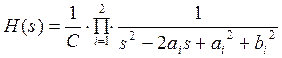                                   (1.2)

где C, a_i и b_i – коэффициенты, которые находим по таблице А2 приложения А (1):

Для фильтра Баттерворта 4го порядка:

С = 0,57735027

-a₀ = 0,4390154575

-a₁ = 1,059877074

±b₁ = 1,059877074

±b₂ = 0,4390154575

Таким образом, передаточная функция имеет вид:

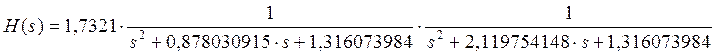
         Для проверки, удовлетворяет ли фильтр 4го порядка заданным значениям рассчитываемого фильтра, необходимо проверить, выполняются ли условия:

|H(jΩ)| = H(s)|_s = jΩ

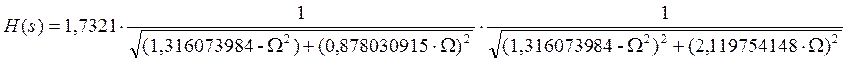Подставляя вместо Ω:

При Ω = 0 получаем H(0) = 1

При Ω = 1 получаем H(1) = 0,86605 > 1 – ε_п = 0,861