ПРИМЕР РАСЧЕТА РЦФ
Проектируется РЦФ нижних частот на основе аналогово-цифровой трансформации по заданным требованиям к неравномерности АЧХ
εп = 0,015 в полосе пропускания с частотами от 0 до fп = 4,8 кГц, отклонению от нуля εп = 0,01 в полосе задерживания (от граничной частоты fз = = 9,6 кГц до f = ∞). Частота дискретизации fд = 48 кГц.
Коэффициенты фильтра должны быть квантованы до m = 24 разрядов (предполагается, что фильтр будет реализован (после испытания на ПЭВМ) на базе микропроцессора DSP-56000). Разрядность входного сигнала ЦФ должна быть 16 (что соответствует использованию 16-ти разрядного АЦП на входе сигнального микропроцессора DSP-56000).
Определить порядок фильтра и системную функцию H(z); рассчитать и построить графики амплитудно-частотной (АЧХ), фазо-частотной (ФЧХ) и импульсной (ИХ) характеристик РЦФ.
Решение.1. Расчёт нормированных "цифровых" граничных частот: wп = fп / fд = 4,8 /48 = 0,1 и wз = fз / fд = 9,6 /48 = 0,2.
2. Расчёт значений коэффициентов затухания: αmax = −20lg[(1−εп)] = −20lg[1− 0,015] ≈ 0,1313 дБ; αmin = −20lgεз = −20lg0,01= 40 дБ.
3. Расчёт коэффициента γбилинейного преобразования: γ= ctg(πwп) = ctg(π⋅ 0,1) = 3,077684.
4. Определение граничной "аналоговой" частоты Ωз полосы задерживания АФ-прототипа:
Ωз = γ⋅ tg(πwз ) = 3,077684⋅ tg(π⋅ 0,2) = 2,236.
5. Определение передаточной функции
H(p) аналогового нормированного фильтра-прототипа нижних частот требуемого
типа. а) Выбираем фильтр Чебышева типа Т с равноволновыми
колебаниями АЧХ в полосе пропускания и равномерным затуханием
в полосе задерживания. б) Расчёт модуля коэффициента отражения |р|% по заданной ве![]() личине αmax: |р| % =100 1 − е−0,23026 ⋅0,1313 ≈ 17,26%.
личине αmax: |р| % =100 1 − е−0,23026 ⋅0,1313 ≈ 17,26%.
При |р| % ≈ 17,26% выбираем (см. табл. 1) ближайший меньший модуль коэффициента отражения, т. е. |р| % = 15%. Отметим, что величине |р|% = 15% соответствует αmax= 0,0988 дБ, т. е. неравномерность затухания в полосе пропускания рассчитываемого фильтра будет несколько лучше, чем требуется. Такой запас необходим, поскольку представление коэффициентов ЦФ с помощью конечного числа разрядов приводит к изменению характеристики затухания. в) Определение вспомогательного параметра L по общей номограмме
(рис. 12).
Для величин |р|% = 15% (αmax= 0,0988 дБ) и αmin = 40 дБ вспомогательный параметр L ≈ 0,04.
г) Определение порядка N передаточной функции АФ-прототипа по номограммам (рис. 13, а и б) для фильтра Чебышева типа Т. Для величин L ≈ 0,04 и Ωз = 2,236 из номограмм порядок 4< N < 5. Принимаем N = 5. д) Запись передаточной функции H(p) в общем виде (см. (22)):
2 2 − 2ai p+ai2 +bi2)], N = 5. H(p) =1/[С(p−a0)∏ (p i=1
е) Определение численных значений коэффициентов передаточной
функции H(p) из таблиц с учётом величин N и |р|%.
Для Т05 (фильтр Чебышева типа Т 5-го порядка) и |р|% = 15% (см. табл. 2) (с округлением шестого знака после запятой):
С = 2,427464; - а0 = 0,540249; - а1 = 0,437071; ±b1 = 0,668079; - а2 = 0,166946; ±b2 = 1,080975. ж) Запись передаточной функции H(p) аналогового нормированного ФНЧ с численными значениями коэффициентов.
Передаточная функция H(p) аналогового нормированного ФНЧ
H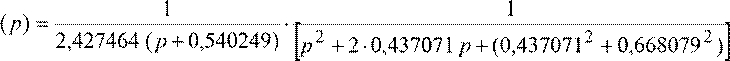 ×
×
×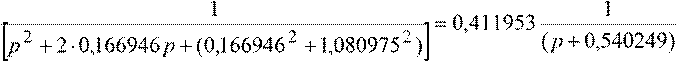 ×
×
× 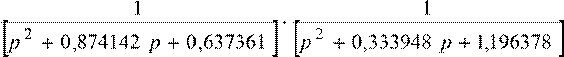 .
.
6. Расчёт и построение АЧХ H(Ω) и коэффициента затухания α(Ω)
АФ-прототипа.
Расчёт и построение АЧХ H(Ω) и коэффициента затухания α(Ω) (после замены р = jΩи вычисления модуля H(jΩ)) АФ-прототипа выполняется на ПЭВМ в К (41…81) точках с шагом по частоте DF = (0,05…0,1). Пользователь (после запуска программы DRF.ехе и щелчка левой клавишей мыши на кнопке "Новый" на полосе инструментов, см. рис.14, вверху) последовательно вводит значения исходных данных: C; γ; N; а0; аi; bi и щёлкает на кнопке "Запомнить" в окне "Параметры РЦФ" (рис. 14, а).При щелчке мышью на соответствующей кнопке ( "АЧХА" и "ЛАЧХА") на экран дисплея выводятся графики функций H(Ω) и α(Ω) (рис. 14, б и г). Если значение коэффициента α(Ω) равно бесконечности (значение АЧХ равно нулю), то принимается значение α(Ω) = 200 дБ.
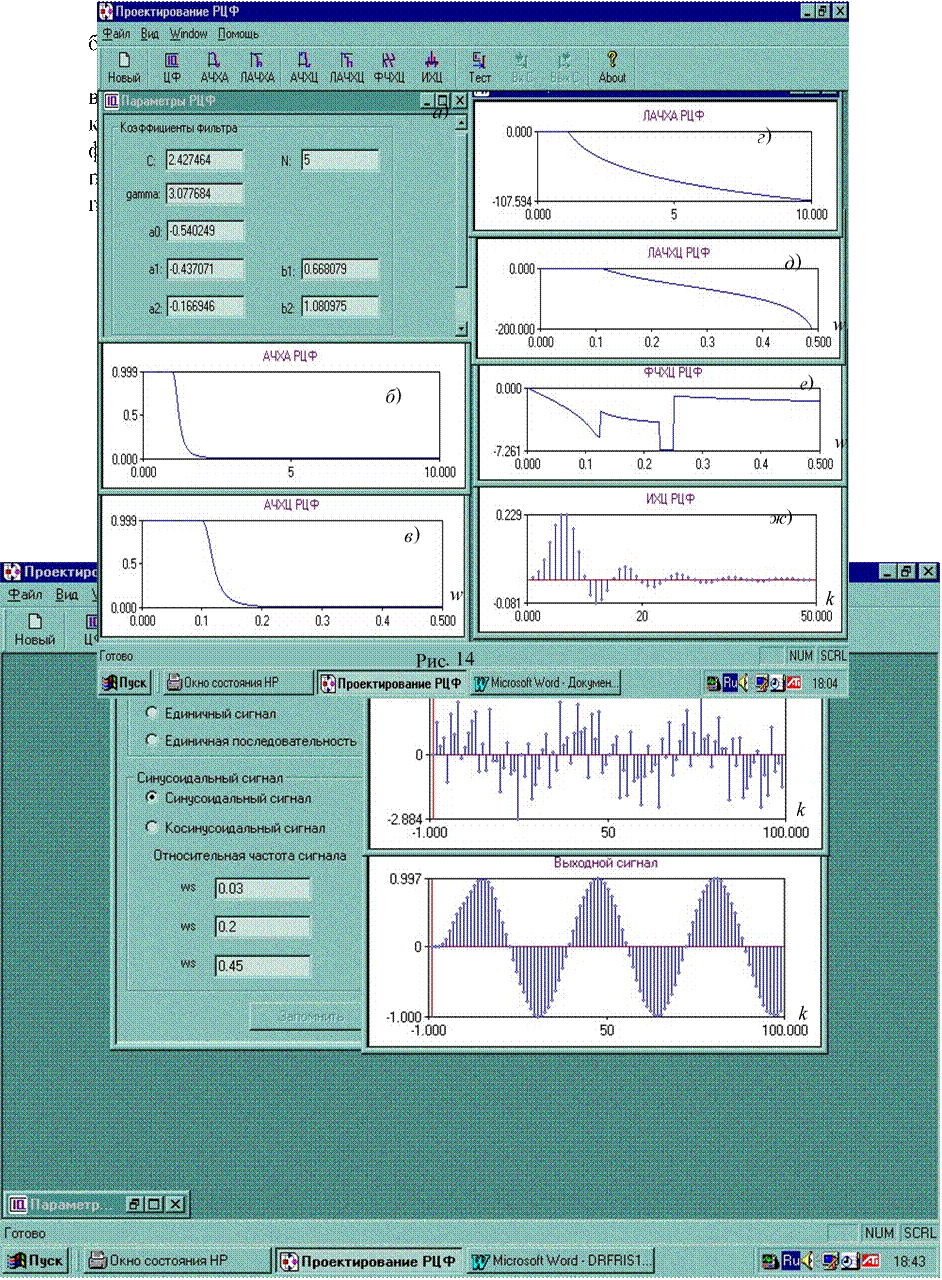 Рис 15 Системная функция
H(z) цифрового фильтра нижних частот определяется с помощью подстановки
p =γ(1− z−1) /(1 + z−1) = 3,077684 (1
− z−1) /(1 + z−1) в выражение H(p):
Рис 15 Системная функция
H(z) цифрового фильтра нижних частот определяется с помощью подстановки
p =γ(1− z−1) /(1 + z−1) = 3,077684 (1
− z−1) /(1 + z−1) в выражение H(p):
![]() H(z) =0,411953γ1+z−−11 1 ⋅ 1−
z−12 + 0,8741421 ⋅γ1−
z−−11 + 0,637361
×
H(z) =0,411953γ1+z−−11 1 ⋅ 1−
z−12 + 0,8741421 ⋅γ1−
z−−11 + 0,637361
×
1−z +0,540249γ1+ z−1 1+ z
× 1 .
![]() γ1 − z−−1 2 + 0,333948 ⋅γ1 − z−−11 + 1,196378
γ1 − z−−1 2 + 0,333948 ⋅γ1 − z−−11 + 1,196378
1 + z 1 1 + z
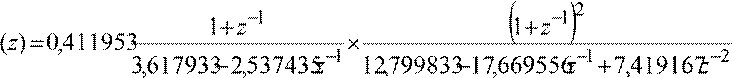 ×
×![]()
![]()
![]() ×11,696303 −16,551522(1+z−1z)−21+ 9,640731z−2 = 0,0000761−
0,1701349+z−1 z−1× × 1+ 2z−−11++0z.579630−2 z−2 ×1−1,4151071+ 2zz−−11++0z,824255−2 z−2 . 1−1,380452z
×11,696303 −16,551522(1+z−1z)−21+ 9,640731z−2 = 0,0000761−
0,1701349+z−1 z−1× × 1+ 2z−−11++0z.579630−2 z−2 ×1−1,4151071+ 2zz−−11++0z,824255−2 z−2 . 1−1,380452z
8. Контрольная проверка устойчивости рассчитанного РЦФ.
![]()
![]()
![]() Полюсы
функции H(z) устойчивого РЦФ должны располагаться внутри
Полюсы
функции H(z) устойчивого РЦФ должны располагаться внутри
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.