Сущность методов и алгоритм многомерного шкалирования. Сжатие признакового пространства

5. Многомерное шкалирование

5.1. Методические указания

5.1.1. Сущность методов и алгоритм многомерного шкалирования

Термин «многомерное шкалирование» (МШ) является синонимом понятия «ординация», т. е. упорядочения. Имеется в виду упорядочение наблюдаемых объектов в m – мерном признаковом (стимульном) пространстве. Также как и в факторном анализе, в МШ появляются латентные признаки, однако, они определяются не на основе интегрирования элементарных признаков, а исходя из различий наблюдаемых объектов и их распределения в некотором теоретическом пространстве.

Методы многомерного шкалирования в статистических исследованиях используются для решения следующие задач:

-  сжатие признакового пространства;

-  визуализация расположения наблюдаемых объектов относительно друг друга в теоретическом пространстве;

-  выявление латентных факторов, предопределяющих пространственное расположение, различие наблюдаемых объектов.

С помощью МШ открывается возможность моделирования сложных явлений, процессов и построения прогнозов их развития.

Всю совокупность методов МШ разделяют на два больших класса: метрические и неметрические.

Метрические методы используются для обработки, анализа количественных данных.

Неметрические методы применяют, когда в качестве исходных выступают неколичественные данные – порядковые, ранговые и т. п.

Принимая во внимание, что данные могут быть количественными или неколичественными, многомерное шкалирование, в зависимости от объекта исследования, имеет несколько различных направлений:

·  анализ стимулов – изучение некоторой совокупности объектов и моделирование их пространственного расположени в соответствии с определенными признаковыми различиями;

·  анализ индивидуальных различий – изучение субъективного восприятия наблюдаемых объектов и их различий;

·  анализ предпочтений – изучение совокупности объектов с учетом существования некоторых идеальных объектов, другими словами, существование представлений об идеальных объектах;

·  анализ идеальных точек – поиск, формальное описание, пространственное отображение идеального положения изучаемых объектов (стимулов).

5.1.2. Представление и первичная обработка данных

В основе построения алгоритмов МШ лежат два типа формальных моделей:

·  дистанционные, в большинстве случаев базируются на евклидовой метрике, при этом описывают различия наблюдаемых объектов – расстояниями (d_ij) в теоретическом шкальном пространстве –

,

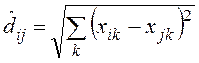          векторные, с их помощью различия объемов аппроксимируются скалярными произведениями векторов, соединяющих начало координат с точками пространственного расположения стимулов –

.

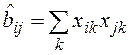При записи моделей МШ используются обозначения:

x_ik, x_jk   –значения k-го признака, наблюдаемые у  i-го и  j-го объектов (стимулов);

_ij, _ij – статистически оцененные меры различия i-го и j-го стимулов.

В практике исследований чаще используются дистанционные модели. Общий алгоритм, базирующийся на подходе Торгерсона, в основе которого лежит дистанционная модель методов МШ, включает следующие шаги:

·  систематизация данных статистического наблюдения, экспертных оценок и т. п., и представление результатов в виде  матрицы различий симметрического вида. На главной диагонали этой матрицы расположены нули (меры различия одних и тех же стимулов), отражающие полное сходство;

·  переход от матрицы различий к матрице с двойным центрированием, которая в последующем позволяет выявлять латентные признаки;

·  определение латентных признаков (F_r) с помощью метода главных компонент, или какого - либо из методов факторного анализа;

·  интерпретация аналитических результатов при необходимости их визуальное (графическое) представление.

Построение матрицы различий (первый шаг) предполагает вначале формирование матрицы исходных данных. Эту матрицу получают, используя оценки экспертов или регистрируя непосредственно признаковые значения исследуемых явлений, процессов в ходе статистического наблюдения.

Экспертные оценки обычно систематизируют в матрице условных вероятностей (матрице идентификаций) или матрице совместных вероятностей.

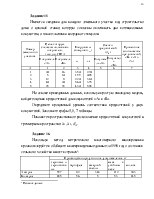
Матрица условных вероятностей представляет относительные данные по узнаванию стимулов. Например, экспертам для узнавания предъявляется стимул А; семьдесят процентов его узнают, двадцать пять процентов – принимают за стимул В, пять процентов за стимул С и т.д. (рис. 5.1а).

Обычно матрица условных вероятностей не симметрическая, поэтому предусматриваются использование определенных методов по приведению ее к симметрическому виду. Простейший метод – когда на главной диагонали проставляются нули, а элементы, равноудаленные от главной диагонали (снизу и сверху от нее), находят как полу сумму исходных значений (рис.5.1.б).