Сущность методов и алгоритм многомерного шкалирования. Сжатие признакового пространства, страница 3

–  поиск улучшенных оценок координат (с использованием формулы Лингоса – Роскома);

–  оценка степени улучшения значений координат стимулов. Если улучшение мало – алгоритм завершается, если улучшение существенно – алгоритм возобновляется, начиная с шага “стандартизировать оценки координат стимулов”.

Кроме анализа стимулов в МШ не редко решаются задачи анализа индивидуальных различий, анализа предпочтений и анализа идеальных точек.

В анализе индивидуальных различий – одновременно обрабатывается несколько матриц различий , по числу экспертов, оценивающих стимулы. В ходе анализа устанавливается не только пространственное расположение стимулов, но и весовые значения экспертов, которые придаются каждой из k – шкал стимульного пространства. Расчеты при этом производятся с использованием модифицированных дистанционных моделей. В большинстве случаев, это взвешенная эвклидова модель, или трех модельная модель Такера.

Анализ предпочтений и анализ идеальных точек в определенной мере связаны. В первом случае оценивается удаленность от представляемого «идеала», во втором – производится оценка координат идеального стимула.

Аналитические цели достигаются применением дистанционной или векторной модели. В ходе анализа определяются координаты стимулов (в т. ч. и идеальных точек), а так же предпочтения экспертов, их суждения об «идеале».

  Более подробно о неметрическом шкалировании и анализе индивидуальных различий, предпочтений и идеальных точек см. в специальной литературе, и в частности «Многомерный статистический анализ в экономике» (под ред. В.Н. Тамашевича), М.: ЮНИТИ, 1999г.

5.2. Примеры решения типовых задач

Пример 1. В табл.5.1 приведены статистические показатели по трем отраслям экономики: Республики Беларусь за 2001г .

Таблица 5.1. Исходные данные

Отрасль	Объем продукции, млр. руб.	Численность работающих, тыс. чел.	Рентабельность продукции, %	Средне месячный уровень заработной платы, тыс. руб.	Кредиторская задолженность,, на конец года, в расчет на один рубль выпуска руб.
Промышленность Сельское хозяйство Строительство	14650 4364.3 1400	1223 606 306	10,8 0,2 8,2	148.4 76,5 157,3	0,264 0,234 0,274
В среднем отраслям	6804,8	711,7	6,4	127,4	0,256

Требуется определить признаки, отражающие различие трех отраслей и показать их пространственное расположение.

В ходе анализа будем использовать следующий метод нормирования: , где  - среднее значение изучаемого признака по трём отраслям, и евклидову метрику для оценки различий отраслей.

Решение

1. В начале проведем анализ стимулов. Нормируем исходные данные:

2,15;   1,72;   1,69 и т. д.

Матрица нормированных значений стимулов принимает вид:

Z=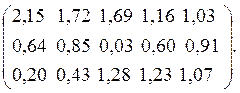

Используя евклидову метрику, определим различия отраслей:

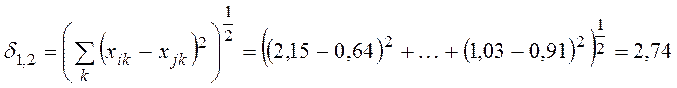
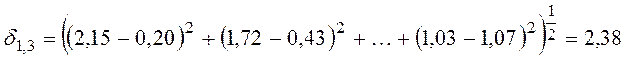
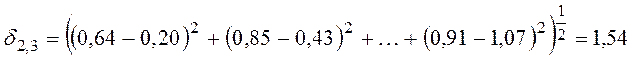
Обобщим метрические данные в исходной матрице различий ():

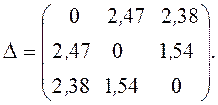
Для получения координат стимулов в теоретическом шкальном пространстве необходимо от матрицы различий  перейти к матрице с двойным центрированием .

Элементы матрицы  исчислим по известной формуле:

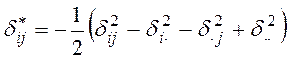, при этом,

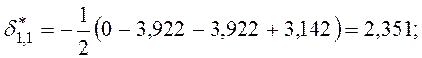
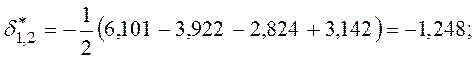
и т.д.

Общий объем вычислений сокращается, с учетом симметричности матрицы с двойным центрированием , в результате получаем:

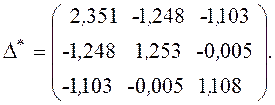
Правильность построения матрицы  подтверждается при суммировании её элементов по каждой строке и каждому столбцу, все суммы равны нулю.

2. Определим координаты стимулов (отраслей экономики). Эта задача решается, исходя из равенства , методом главных компонент, или каким-либо из методов факторного анализа (см. п. 4.1).

Используя метод главных компонент, получим следующую матрицу:

X=.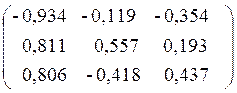

Каждый элемент этой матрицы x_ij – значение j -ой главной компоненты для i -ой отрасли.