|
А |
В |
С |
Д |
|
А |
В |
С |
Д |
||
А |
0,70 |
0,25 |
0,05 |
0,00 |
А |
0 |
0,28 |
0,08 |
0,01 |
|
|
В |
0,30 |
0,50 |
0,15 |
0,05 |
В |
0,28 |
0 |
0,28 |
0,04 |
|
|
С |
0,10 |
0,40 |
0,40 |
0,10 |
С |
0,08 |
0,28 |
0 |
0,15 |
|
|
Д |
0,02 |
0,03 |
0,20 |
0,75 |
Д |
0,01 |
0,04 |
0,15 |
0 |
(а) (б)
Рис.5.1. Матрица условных вероятностей (1а) и полученная из нее матрица различий (Δ).
Матрица совместных вероятностей отражает взаимодействие стимулов (i, j). Она содержит согласованные данные и всегда симметрическая.
Значения признаков исследуемых явлений, процессов первоначально представляются в виде матрице, которую называют матрицей мер различия профилей. Переход от нее к матрице различий предусматривает нормирование, а затем исчисление мер признаковых различий стимулов.
На первом шаге выполняется нормирование исходных значений признаков с помощью одного из следующих приемов:
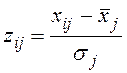 ,
, ![]() ,
, ![]() .
.
Меры различия находят по метрическим формулам. Среди них наиболее распространены следующие:
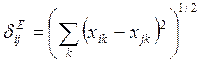 - евклидова
метрика,
- евклидова
метрика,
![]() -
квадрат евклидова расстояния,
-
квадрат евклидова расстояния,
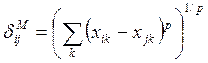 - метрика
Минковского,
- метрика
Минковского,
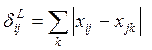 -
метрика city - block.
-
метрика city - block.
Меры различия
обобщаются в матрице различий (![]() ) симметрического
вида (рис.5.1 б).
) симметрического
вида (рис.5.1 б).
Второй шаг
алгоритма –
переход от матрицы различий (![]() ) к матрице с
двойным центрированием (
) к матрице с
двойным центрированием (![]() *) – осуществляется
по формуле:
*) – осуществляется
по формуле:
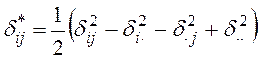 , где,
, где, ![]() - средняя для
характеристик различий в j - х столбцах i - й строки, возведенных в квадрат:
- средняя для
характеристик различий в j - х столбцах i - й строки, возведенных в квадрат: 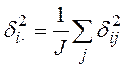 ;
;
![]() - средняя для
характеристик различий в i - х строках j - го столбца, возведенных в квадрат:
- средняя для
характеристик различий в i - х строках j - го столбца, возведенных в квадрат: 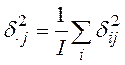 ;
;
![]() - средняя величина для
квадратов характеристик различий всей матрицы различий
- средняя величина для
квадратов характеристик различий всей матрицы различий ![]() :
: 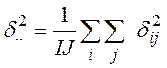 .
.
Правильность построения матрицы с двойным центрированием легко проверяется: суммы ее элементов, полученные по любой строке или столбцу должны быть равны нулю.
Для матрицы с двойным центрированием существует равенство:
![]() , (5.1)
, (5.1)
где X – матрица значений обобщенных
(латентных) признаков1. Важно учитывать, что их определенность
обусловливается не признаковым составом ![]() ,
как в факторном анализе, а составом стимулов (обычно – наблюдаемых объектов).
,
как в факторном анализе, а составом стимулов (обычно – наблюдаемых объектов).
На третьем шаге алгоритма, исходя их равенства (5.1) находят сами латентные признаки. С этой целью используют методы главных компонент или факторного анализа (главных факторов, центроидный, максимального правдоподобия и т. п.).
На завершающем, четвертом шаге алгоритма МШ производится интерпретация полученных аналитических результатов и их визуальное представление. При объяснении выходных данных МШ исходят из того, что название латентных признаков формируется структурой наблюдаемых объектов (стимулов), а не признаков, как в факторном анализе.
Графическое
изображение стимульного пространства, с погружением в него стимулов строится на
основе значений одного - трех латентных признаков ![]() ,
как правило, первых, имеющих наибольшую информативную нагрузку.
,
как правило, первых, имеющих наибольшую информативную нагрузку.
В отличие от алгоритма обработки количественных данных методами МШ, алгоритм обработки неколичественных данных имеет дополнительные шаги, они сводятся к следующим операциям:
–
![]() оцифровки неколичественных данных;
оцифровки неколичественных данных;
–
![]() получение стартовой конфигурации
стимулов;
получение стартовой конфигурации
стимулов;
–
![]() стандартизации текущих координатных
оценок;
стандартизации текущих координатных
оценок;
–
![]() вычисление различий стимулов по
теоретическим данным;
вычисление различий стимулов по
теоретическим данным;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.