После задания всех необходимых параметров, щёлкнем на кнопке OK. Программа выдаст окно для задания вида дискриминантной функции. В этом окне (рис.7.3.4) необходимо ещё раз уточнить набор дискриминантных переменных (в нашем примере это X1, X2, X3) и выбрать метод отбора дискриминантных переменных.
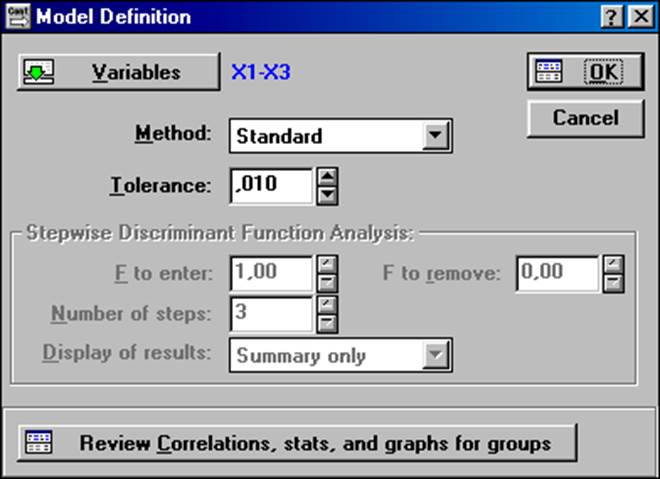
Рис. 7.3.4.Окно для определения методов построения модели
В системе STATISTICA реализованы следующие методы дискриминации:
Standard – стандартный метод, который предполагает использование всех дискриминантных переменных, первоначально указанных пользователем (см. рис.7.3.3), независимо от уровня их информативности.
Forwardstepwise – прямая процедура пошагового отбора переменных, начиная с переменной, обеспечивающей наилучшее различение множеств. На каждом шаге этого алгоритма отбирается очередная переменная, которая в сочетании с ранее отобранными, даёт наилучшее различение групп.
Backwardstepwise – обратная процедура пошагового отбора дискриминантных переменных; когда на первом шаге алгоритма все переменные включаются в дискриминантную функцию. На каждом последующем шаге происходит исключение из набора той переменной, которая вносит наименьший вклад в различение множеств.
В нашем примере был выбран стандартный метод, то есть все переменные (X1, X2, X3) включены в состав дискриминантной функции.
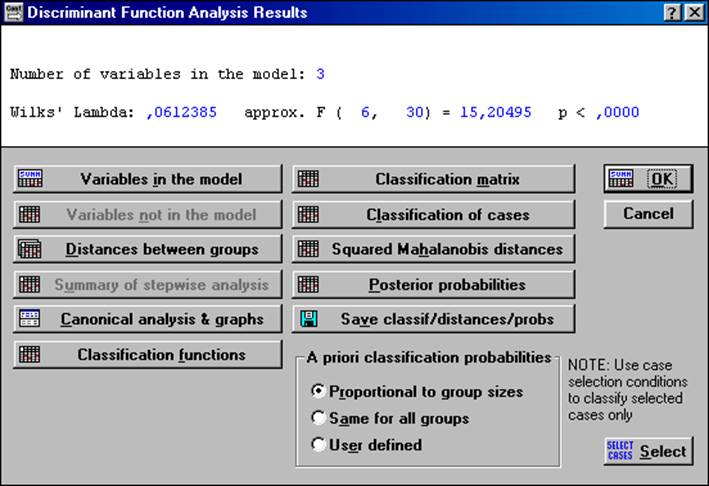
Рис. 7.3.5. Окно для проведения анализа дискриминантных функций.
На следующем шаге проведения дискриминантного анализа нам необходимо оценить коэффициенты дискриминантных функций. Для этого в окне на рис.7.3.5 щёлкнем на кнопку ClassificationFunctions(классификационные, т.е. дискриминантные функции).
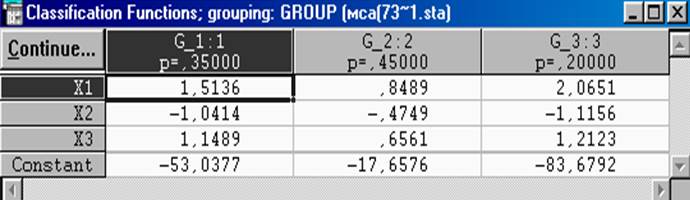
Рис. 7.3.6. Расчётные значения коэффициенты дискриминантных функций
Полученные результаты (рис.7.3.6) позволяют нам записать выражения всех трёх дискриминантных функций:
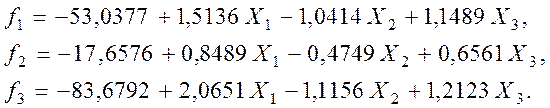
Это так называемые линейные дискриминантные функции Фишера, с которыми подробно можно познакомиться в специальной литературе [12,25].
На основе рассчитанных классификационных функций по определённому правилу производится повторная классификация объектов всех трёх подмножеств [12]. Чтобы увидеть результаты этой процедуры, нужно в окне (рис.7.3.5) щёлкнуть на кнопку ClassificationMatrix.
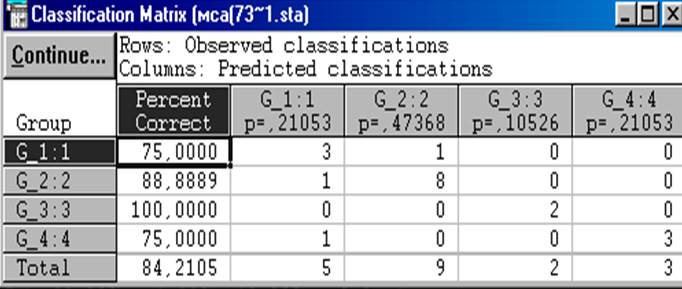
Рис.7.3.7. Результаты применения классификационных функций
На рис.7.3.7 мы видим, что произошли изменения в первоначальном составе подмножеств. Например, с учётом применения классификационных функций в первую группу отнесены три объекта, хотя первоначально в ней находились четыре объекта. Следовательно, процент корректной классификации составляет 75% (3/4×100). Аналогично трактуются и другие результаты. Средний по всем группам процент корректной классификации составил приблизительно 84,2% (последняя строка таблицы). Это свидетельствует о хорошем качестве классификации.
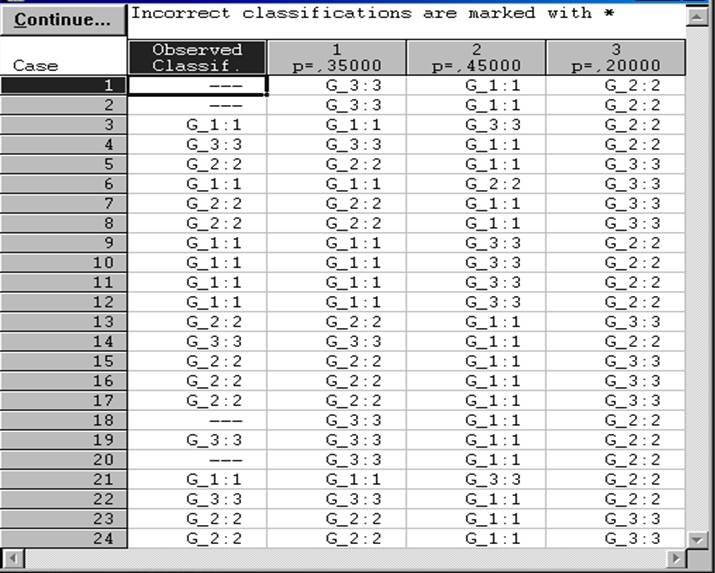
Рис.7.3.8.
Результаты классификации объектов трёх подмножеств банков на основании
классификационных функций ![]() .
.
Чтобы получить полную картину классификации, т.е. узнать какие объекты и на каком основании были отнесены к соответствующему множеству, нужно в окне (рис.7.3.5) выбрать процедуру Classificationofcases. В раскрывшемся окне (рис.7.3.8) мы видим детальную картину классификации. Поясним некоторые её фрагменты. В первой графе таблицы указаны номера объектов анализируемой совокупности; во второй графе приведены номера тех групп , к которым мы первоначально причислили изучаемые объекты (прочерками отмечены четыре объекта, которые мы по результатам кластерного анализа не отнесли ни к одной из выделенных групп). Далее для примера рассмотрим ситуацию с третьим объектом. На первом шаге мы причислили его к первому подмножеству, а по результатам вычислений на базе классификационных функций самой высокой оказалась вероятность его принадлежности к третьему подмножеству (р=0,45). Именно на основании этой (максимальной) вероятности он и был причислен к нему. Для всех остальных случаев рассуждения аналогичны.
В заключение отметим, что пользователь при желании может получить геометрическую интерпретацию результатов классификации, т.е. на графике увидеть расположение анализируемых объектов в пространстве дискриминантных функций.
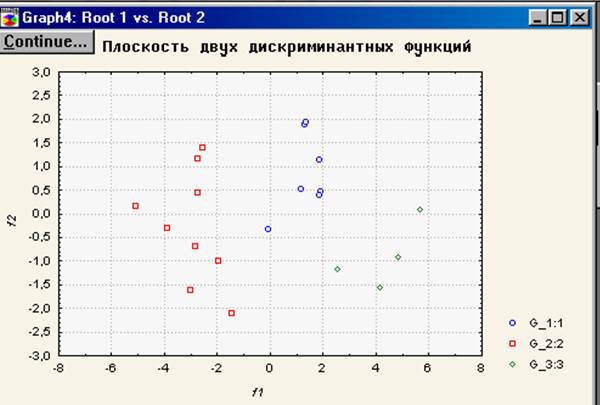
Рис.7.3.9. Диаграмма рассеивания 20-ти наблюдаемых объектов в координатной системе двух дискриминантных функций.
Для этого нужно в окне (рис.7.3.5) выбрать процедуру Canonicalanalysis & graphs(канонический анализ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.