Факторный анализ. Метод максимального правдоподобия Д. Лоули и Д. Максвелла. Метод минимальных остатков Г. Хармана

могло произойти из-за допускаемой грубости итеративных решений и округлений. В скобках приведены первоначально принятые величины общностей для каждого признака. Общности и характерности совместно полностью представляют дисперсии признаков, равные единице, в общем: .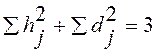

4.3 Реализация методов факторного анализа на компьютере

Рассмотрим пример проведения факторного анализа с использованием модуля Многомерные исследовательские методы - Factoranalysisв пакете Statistica на основании  исходных данных, представленных в таблице 4.9.

Таблица 4.9 – Экономические характеристики финансовой деятельности организаций территориальных объектов Республики Беларусь в 2009 г.

Здесь: Х₁ — уровень рентабельности реализованной продукции, %; Х₂ — удельный вес убыточных организаций, %; Х₃ — кредиторская задолженность в процентах к дебиторской; Х₄ — просроченная кредиторская задолженность, %; Х₅ — инвестиции в основной капитал в % к предыдущему году.

После ввода исходных значений анализируемых переменных в стартовой панели анализа данных выбираем модуль «Факторный анализ» (Factoranalysis).

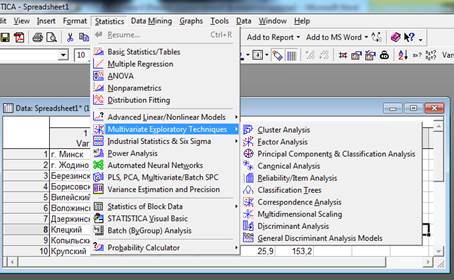
В открывшемся окне (рис. 4.1) выбираем переменные (Variables), которые будут использованы при формировании новых факторов, и нажимаем ОК.

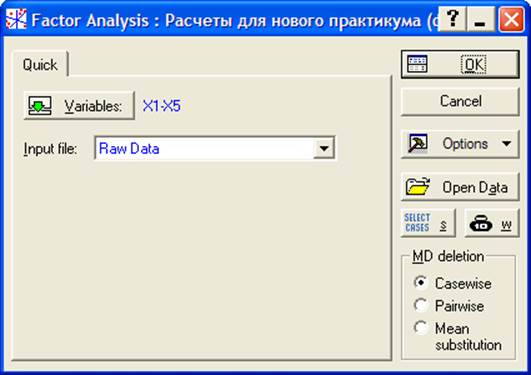
Рисунок 4.1 Выбор переменных для проведения факторного анализа

Начнем расчеты с использования метода главных компонент. Для этого в диалоговом окне (рис. 4.2) выберем метод анализа Principalcomponents и нажимаем OK.

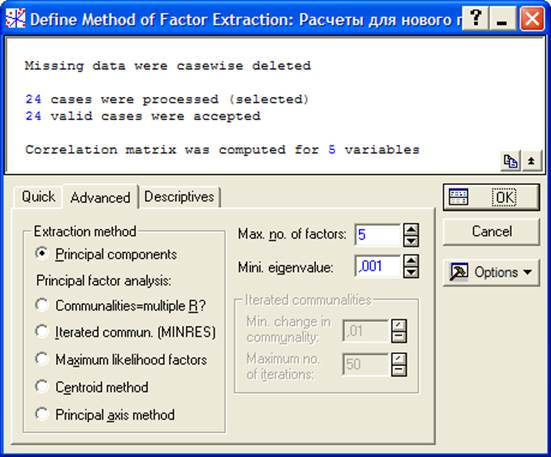
Рисунок 4.2 Диалоговое окно факторного анализа с выбранным методом главных компонент

В диалоговом окне на рисунке 4.2 видно, что максимальное число выделяемых компонент (Maz. no. offactors) равно 5. А минимальное собственное значение (Mini.eigenvalue) равно 0,001. После нажатия клавиши OKоткрывается окно для выбора и просмотра результатов анализа по методу главных компонент (рисунок 4.3). Для данного примера вычислены все пять собственных значения корреляционной матрицы:

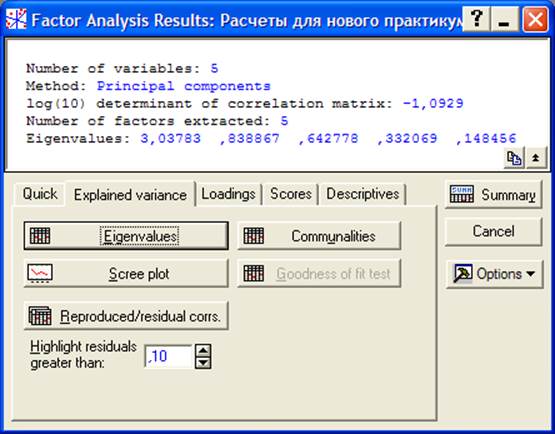
Рисунок 4.3 Выбор и просмотр результатов анализа по методу главных компонент

По собственным значениям можно оценить вклад каждой главной компоненты в объясненную суммарную дисперсию исходных переменных (рисунок 4.4)

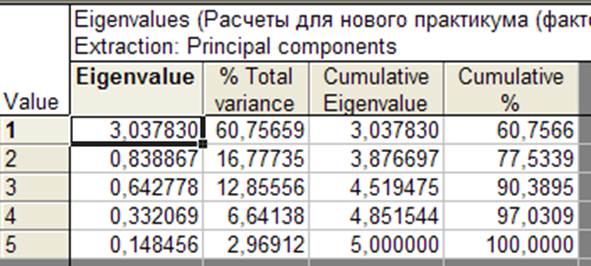
Рисунок 4.4. Собственные значения корреляционной матрицы и доли дисперсий исходных переменных, объясненных соответствующими компонентами

На рисунке 4.4 видно, что первые три главные компоненты объясняют более 90% суммарной дисперсии исходных переменных

Для вычисления матрицы факторных нагрузок каждой исходной переменной на главные компоненты выбираем в меню окна (рисунок 4.5) опцию Summary: Factorloadings.

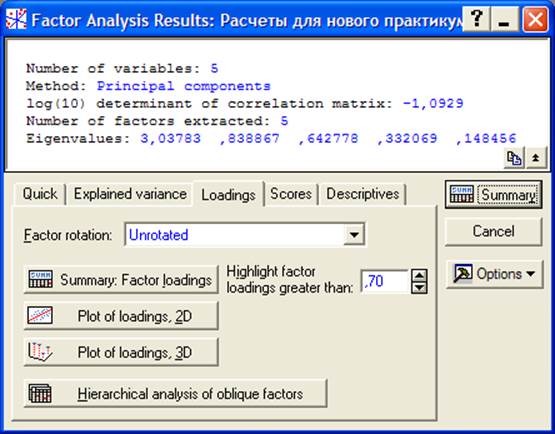
Рисунок 4.5 Меню факторного анализа

На экране появится матрица факторных нагрузок для всех главных компонент (рисунок 4.6), в которой красным цветом отмечены большие факторные нагрузки переменных на данных фактор (главную компоненту). На основании этой матрицы и должны быть сформулированы исследователем названия главных компонент.

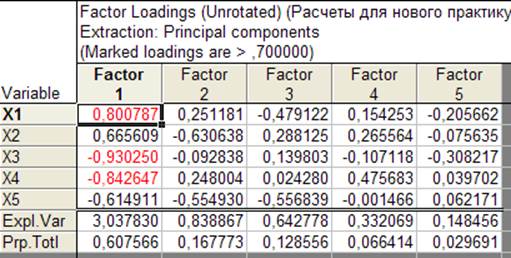
Рисунок 4.6 Матрица факторных нагрузок

Как правило, для удобства последующей визуализации результатов факторного (компонентного) анализа выбирают первые две главные компоненты. В данном примере на них приходится 77,5 % объясненной суммарной дисперсии исходных переменных (рисунок 4.4).

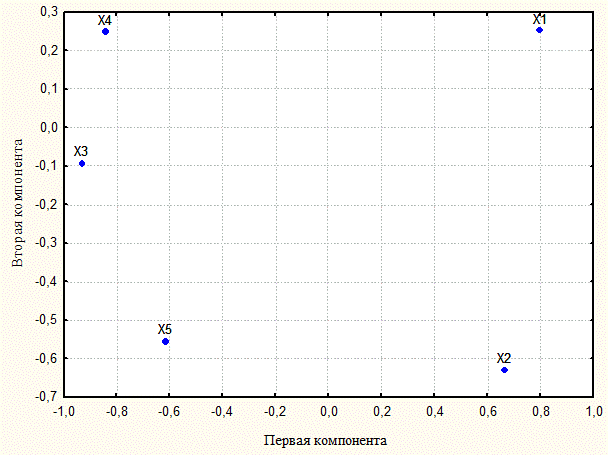
Рисунок 4 7 Факторные нагрузки исходных переменных на первые две главные компоненты

Для вычисления значений главных компонент для каждого наблюдаемого объекта (таблица 9) в меню факторного анализа (рисунок 4.5) необходимо выбрать опцию Scoresивкладку Factor scores. На рисунке 4.8

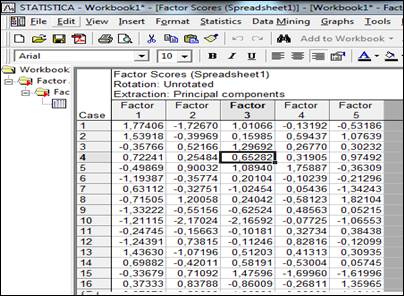
Рисунок 4.8 Значения главных компонент для объектов наблюдения

Если полученные главные компоненты плохо поддаются экономической интерпретации на основании матрицы факторных нагрузок, то можно попробовать процедуру вращения Factorrotation (рисунок 4.5).

При проведении факторного анализа в пакете Statistica выполняются такие же процедуры как и при компонентном анализе.

Контрольные задания

Задание 1

По двенадцати промышленным предприятиям имеются данные об уровне заработной платы – Х₁ (дол. США) и размеру получаемой за месяц прибыли в расчете на одного работника – Х₂ (дол. США):

Представьте результаты статистического наблюдения предприятий в двумерной системе координат, предположительно покажите векторы, которые бы обобщали распределение значений признаков Х_1, Х_2.

Проведите компонентный анализ, выделив две главные компоненты и рассчитайте матрицу факторных нагрузок.

Задание 2

По данным экспертных опросов покупателей натуральных соков построена