Метод канонических корреляций. Пример решения типовой задачи. Проведение канонического анализа на компьютере

8. Метод канонических корреляций

8.1. Методические указания

8.2. Пример решения типовой задачи

8.3. Проведение канонического анализа на компьютере

8.4. Контрольные задания

8. Метод канонических корреляций

8.1. Методические указания

Метод канонических корреляций –статистический метод анализа связей между массовыми общественными явлениями и процессами, применяемый в том случае, когда рассматриваются несколько независимых переменных – и несколько результативных показателей – То есть, канонический корреляционный анализ можно рассматривать как вариант распространения парной корреляции на случай двух многомерных величин.

Важнейшим достоинство метода канонических корреляций является то, что при его применении не требуется подтверждение отсутствия корреляции, как в группе зависимых переменных (), так и в группе независимых переменных ().

Цель применения метода – поиск максимальных корреляционных связей между факторными и результативными переменными.

Исходные данные в анализе канонических корреляций представляются в следующем виде:

Наблюдаемые объекты	X1	X2	....	Xq	Y1	Y2 ...	Yp
1	x11	x12	....	x1q	y11	y12...	y1p
2	x21	x22	....	x2q	y21	y22...	y2p
3	x31	x32	....	x3q	y31	y32...	y3p
...	...	...	...	...	...	...	...
n	xn1	xn2	....	xnq	yn1	yn2...	ynp

Х₁ , Х₂ ... Х_q  – независимые переменные  (факторные признаки);

Y₁ , Y₂ ... Y_p  – зависимые переменные (результативные признаки).

В ходе канонического корреляционного анализа оценивается теснота связи между новыми каноническими переменными  U  и  V, вычисляемыми по формулам:

U = a₁X₁ + a₂X₂ + ... + a_qX_q;

V = b₁Y₁ + b₂Y₂ + ... + b_pY_p.                                                        (8.1)

По аналогии с парной корреляцией, теснота связи между каноническими переменными оценивается при помощи канонического коэффициента корреляции  r:

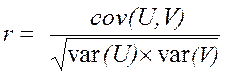,                                                            (8.2)

где  cov(U, V) - ковариация канонических переменных U и V;

 – вариации (дисперсии) канонических переменных. Один из возможных вариантов расчёта:

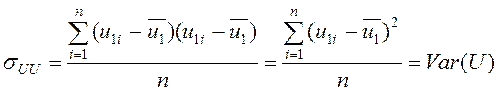;       (8.3)

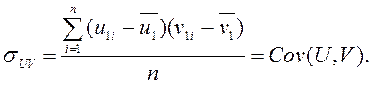                             (8.4)

В зависимости от того, какие значения принимают коэффициенты  a_i  и  b_j   в выражении (8.1), будут изменяться значения канонических переменных и канонический коэффициент корреляции.

Одна из основных задач анализа канонических корреляций, заключается в том, чтобы найти такую пару значений канонических переменных, которой будет соответствовать максимальный канонический коэффициент корреляции.

... ... ... ... ... ... ... ... ... ... ... ...

Для вычисления канонических коэффициентов корреляции необходимо, прежде всего, определить матрицы ковариаций исходных переменных. Запишем расширенную матрицу ковариаций для обеих групп переменных:

S = .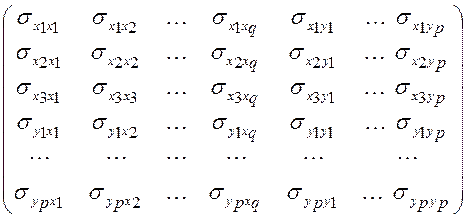

Матрица  S  фактически разделена на четыре части, которые можно обозначить следующим образом:

S = 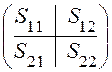, где  S₁₁ - ковариационная матрица исходных факторных переменных  Х₁₂ ,... Х_q размерности (q ´ q),