1. Рассчитаем первый канонический коэффициент корреляции и проверьте его значимость с помощью χ2 - критерия Бартлетта.
2. Оценим коэффициенты канонических переменных для стандартизованных значений исходных переменных: X1, X2, X3, и Y1, Y2.
3. На основании результатов расчетов, выполненных в пп.1-2, определим, какая из линейных комбинаций индексов позволяет наилучшим образом предсказать сводный индекс результативных показателей (изменение потребительских цен и вкладов населения). Все необходимые расчёты выполним на компьютере с использованием пакета программ STATISTICA.
Решение:
В системе STATISTICA метод канонических корреляций реализуется при помощи модуля Canonocal Analis. Введём значения всех исходных переменных в электронную таблицу и сохраним эти данные в файле с именем Primer. Откроем окно выбора модулей и выберем модуль CanonicalAnalysis(рис.8.1)
Рис.8.1. Окно выбора аналитического модуля
После выбора модуля на экране появится окно (рис. 8.2), в котором необходимо указать имена переменных, принадлежащих первому ( First List) и второму ( Second List) множеству анализируемых признаков.
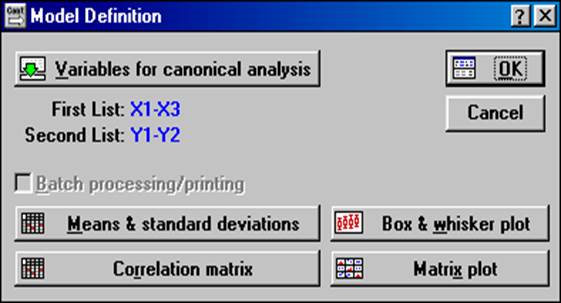
Рис.8.2. Окно диалога для ввода переменных двух множеств
В нашем примере к первому множеству (независимые переменные) относятся переменные Х1, Х2, Х3, а ко второму множеству (зависимые переменные) – Y1 и Y2. Нажимаем кнопку OK, чтобы продолжить анализ или предварительно просмотрим матрицу парных корреляций для исходных переменных (рис.8.3)
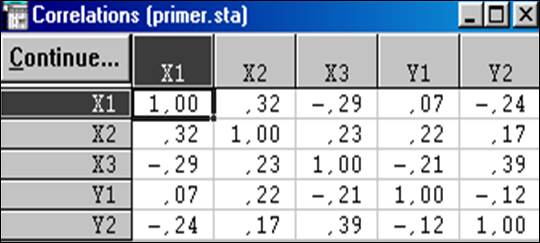
Рис.8.3. Матрица парных корреляций (R).
В окне основных процедур канонического анализа (рис. 8.4) видны первые результаты: максимальный канонический коэффициент корреляции (R=0,445) и его оценка по c2–критерию (c2=2,829).
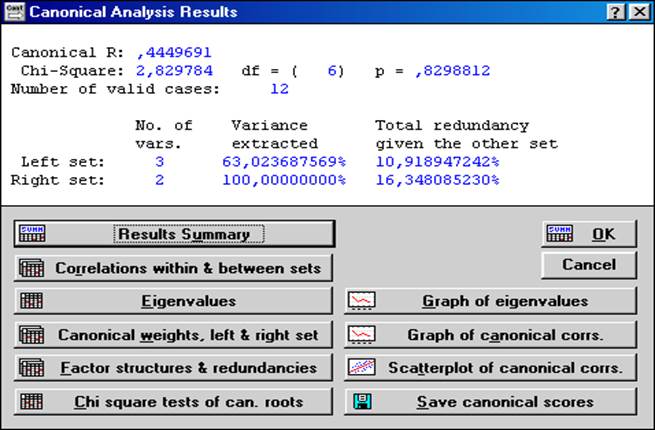
Для того, чтобы продолжить анализ, последовательно выберем, например, процедуры Eigenvalues(собственные значения), Canonicalweights, left & rightset (канонические веса для левого и правого множеств).
В развернувшемся
окне (рис.8.5) мы видим два собственных числа матрицы C (
):
и 
Кроме
того, показаны два варианта (Root 1 и Root 2) канонических весовых
коэффициентов для переменных обоих множеств.
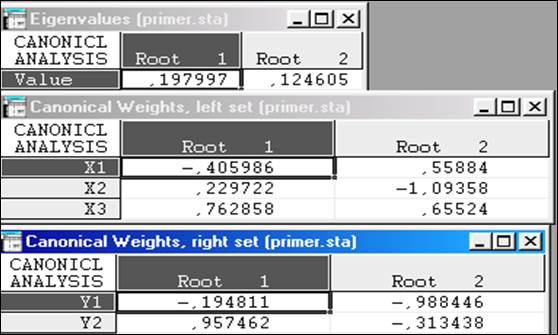
Рис.8.5. Собственные числа и коэффициенты канонических переменных.
Судя по данным на рис. 8.5, можем записать, как выглядят канонические переменные и соответствующие им канонические коэффициенты корреляции:
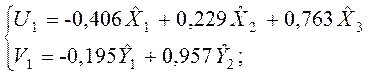r1=0,445 c2=2,83;
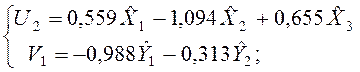r2=0,354 c2=1,06.
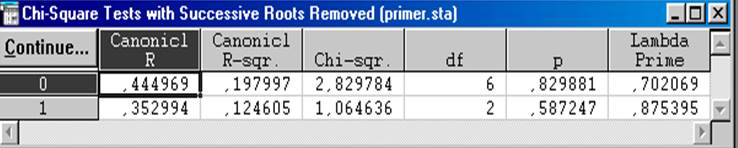
Рис.8.6. Канонические коэффициенты корреляции и их оценки
Для проверки гипотезы о значимости канонических коэффициентов необходимо сравнить расчетные значения (рис. 8.6) с табличным для уровня значимости α = 0,01 c2кр.= 16,80 для шести степеней свободы и c2кр.= 9,2 для двух степеней свободы, т.е. проверяемая гипотеза о равенстве канонического коэффициента корреляции нулю принимается. Следовательно, первый и второй канонические коэффициенты корреляции незначимы. Связь между множествами переменных (Y1, Y2) и (X1, X2, X3, X4) средняя, так как r1=0,445.
Судя по коэффициентам канонических функций, самую большую информационную нагрузку в определении тесноты связи имеют переменные X3 и Y2.
В сложившейся ситуации можно рекомендовать исследователю либо изменить набор исходных переменных, дополнив их более информативными, либо увеличить число наблюдений (n).
8.4. Контрольные задания
Задание 1
На основании нижеприведенных данных по группе предприятий рассчитайте матрицу парных коэффициентов корреляции для последующего проведения канонического анализа:
|
Номер объекта |
I-ое множество переменных |
II-ое множество переменных |
|||
|
Y1 |
Y2 |
Х1 |
Х2 |
Х3 |
|
|
1 2 3 4 5 |
23,0 25,0 25,2 21,0 24,5 |
19,0 12,0 13,4 9,2 14,0 |
570 860 1150 610 502 |
19,4 21,6 28,8 20,5 23,3 |
6,7 13,3 12,2 8,4 6,8 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.