Метод канонических корреляций. Пример решения типовой задачи. Проведение канонического анализа на компьютере, страница 6

Номер предприятия	X1	X2	X3	Y1	Y2
1	-10	120	105,0	25,5	25,0
2	-2	145	110,0	14,8	34,0
3	12	110	104,2	45,3	110,0
4	8	110	100,0	74,5	215,0
5	14	135	98,6	60,0	87,0
6	-7	75	130,0	80,0	135,0
7	-20	80	115,0	65,3	145,0
8	-3	95	101,0	64,1	180,0
9	15	125	95,0	34,5	94,5
10	10	140	94,2	46,3	120,0
11	2	90	94,8	33,4	84,3
12	-17	81	120,0	85,5	180,0
13	5	90	105,0	75,3	65,2
14	3	124	104,0	40,0	170,1
15	-6	80	113,5	80,2	210,0
16	6	65	108,6	35,0	65,0
17	-13	45	118,0	64,0	190,0
18	-25	60	108,0	75,0	285,0
19	4	95	101,0	45,5	210,0
20	8	115	115,0	54,8	250,4

Здесь: 

X₁   –  средний процент снижения себестоимости продукции, %;

X₂   – оборачиваемость оборотных средств, дней;

X₃ – индекс производительности труда рабочего, %;

Y₁   – удельный вес экспорта в объёме реализованной продукции, %;

Y₂ – прибыль на одного работника, тыс. ден. един.

На основе анализа полученных коэффициентов канонических переменных, выберите наименее информативную из числа независимых переменных. Удалив выбранную переменную, повторите расчёты канонических переменных и максимального канонического коэффициента корреляции. Оцените существенность его изменения для усечённого набора переменных.

Необходимые расчёты выполните на компьютере с использованием пакета STATISTICA.

Задание 6

Матрица парных коэффициентов корреляции, рассчитанная для двух групп переменных равна:

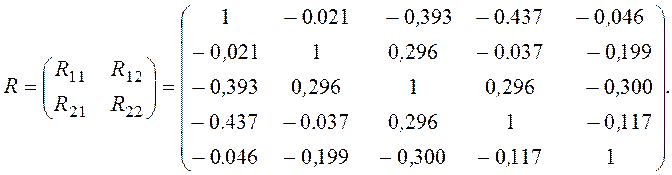
Вычислите собственные значения матрицы С:  и поясните полученные результаты.

Задание 7

На основании собственных значений и собственных векторов матрицы С (см. задание 6) рассчитайте оценки вектора коэффициентов канонической переменной  и максимальный коэффициент канонической корреляции для двух групп переменных.

Задание 8

По результатам выполнения задания 5 рассчитайте значения канонических переменных  U  и  V  для каждого наблюдаемого объекта.

Покажите на графике расположение этих объектов в пространстве канонических переменных. Расчёты выполните на компьютере с помощью пакета EXCEL.

Задание 9

Используя исходные данные, приведенные в задании 5, а также рассчитанные на их основе значения канонических переменных, проведите методом иерархического кластерного анализа классификацию 20-ти объектов: а) по значениям исходных переменных; б) по значениям каноничиских переменных.

Сравните полученные результаты двух классификаций. Оцените каждый из вариантов классификации с помощью одного из функционалов качества [23].

Задание 10

Воспользовавшись приведёнными ниже ковариационной и корреляционной матрицами, вычисленными для одной и той же выборки, определите коэффициенты канонической корреляции для двух множеств переменных (X₁, : X₂ – первое множество; Y₁,  Y₂ – второе множество):

.

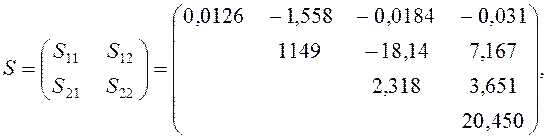
Сравните полученные значения максимальных коэффициентов канонической корреляции, поясните их смысл и оцените оба коэффициента по χ²- критерию Бартлетта.

Задание 11

В ходе проведения канонического анализа были получены собственные числа и собственные векторы матрицы С:

:

;

Вычислите значения соответствующих канонических коэффициентов корреляции и оцените их значимость по критерию Бартлетта.