Метод канонических корреляций. Пример решения типовой задачи. Проведение канонического анализа на компьютере, страница 3

Номер предприятия	X1	X2	X3	Y1	Y2
1 2 3 4 5 6 7 8 9 10	0,25 0,23 0,31 0,28 0,34 0,17 0,11 0,26 0,35 0,28	175 105 120 112 95 75 110 130 85 103	2560 2100 1865 1640 1950 2100 2350 1645 2125 1480	10.1 8.6 9.5 9.0 7.6 11.5 12.0 6.8 8.5 9.4	45 50 68 90 70 65 85 94 76 50

Здесь:

Y₁ - производительность труда, млн. ден.ед./чел;

Y₂ – процент сертифицированной продукции;

х₁ - трудоемкость единицы продукции, чел-час.;

х₂ - оборачиваемость оборотных средств, дней;

х₃- фонд оплаты труда работающих, млн. ден. ед.:

Решение:

Для определения матрицы парных корреляций в начале рассчитаем сначала средние значения исходных переменных:

Матрица парных коэффициентов корреляции для обеих групп равна:

R =

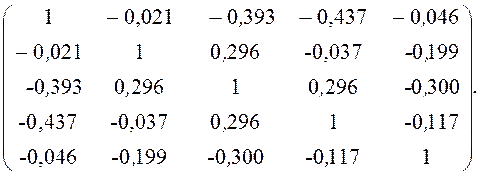
Вспомогательные матрицы  (  и  )  соответственно равны:

,  .

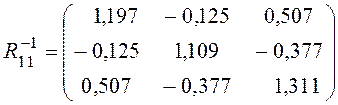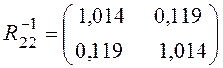На следующем шаге алгоритма вычислим собственные числа и собственные векторы матрицы   Ее размерность в нашем примере будет (2´2),  следовательно, она имеет два собственных числа и два собственных вектора:

.

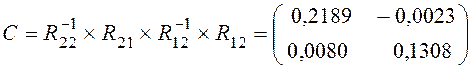Для нахождения собственных чисел составим характеристический многочлен    и  вычислим его  корни:

.

Решая данное уравнение, получим два корня:

Далее для каждого    рассчитаем собственный вектор B_j. Для этого воспользуемся выражением:

Вычислим первый собственный вектор  (B₁ ) для  

                    

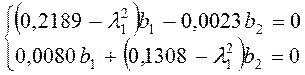
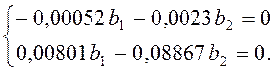
Для получения нетривиальных решений системы уравнений зададим

b₂ =1, тогда  b₁ =11,07.

Вычислим второй собственный вектор (В₂ )  для :

                    

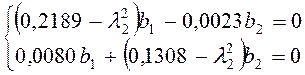
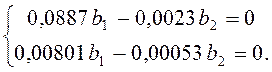
Аналогично зададим  b₂ =1,000  тогда  b₁ =0,026.

Занесём рассчитанные собственные числа и собственные (характеристические) векторы матрицы  С в следующую таблицу:

Корень	Характеристический вектор
	11,07 0,026	1,0 1,0

Канонические коэффициент корреляции равны:

;             

Чтобы найти векторы коэффициентов  A_j, подставляем соответствующие значения   в выражение (8.6). Первый вектор  (A₁)_, соответствующий первому каноническому коэффициенту () , равен:

.

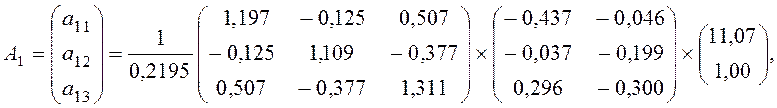
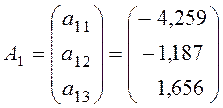Аналогичным образом вычислим второй вектор А₂:

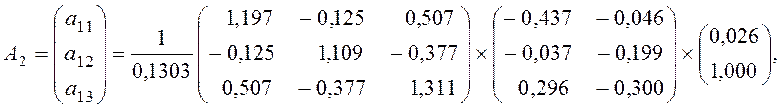
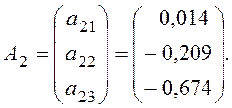
Итак, максимальный коэффициент канонической корреляции равен 0,469. Ему соответствует пара канонических переменных:

.

Второму коэффициенту канонической корреляции r₂ = 0,361 соответствует пара канонических переменных:

,

.

Так как векторы коэффициентов канонических переменных вычислены на основании матрицы парных корреляций (R) они будут относиться к стандартизованным значениям исходных переменных .

8.3. Проведение канонического анализа на компьютере

Пример 1

Динамика макроэкономических показателей в Республике Беларусь сравнению с базисным характеризуется следующими индексами:

Месяц	Индексы, %
	производства			потребительских цен, %	Вкладов  населения, %
	промышленность	сельское хозяйство	транспорт
	X1	X2	X3	Y1	Y2
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь	98,4   96,0 100,5 104,0 108,0 110,0 101,0   99,0 109,0 115,0 120,0 121,0	99,5   98,0 106,0 113,0 124,0 108,6 115,0 122,8 135,5 130,0 121,8 101,3	101,8 105,0 112,0 124,0 126,0 124,0 120,5 115,0 110,3 107,0 100,5   99,8	140,7 118,7 110,2 128,6 128,7 119,5 126,6 153,4 125,5 125,7 140,5 131,3	105,2 119,2 130,6 129,6 118,1 118,5 173,5 132,5 104,4 146,4 115,1 106,9