Приближенные методы решения задач математической физики. Методы коллокации, Ритца, Галеркина, конечных элементов

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Дальневосточный государственный университет

А.Г. КОЛОБОВ, ЛА. МОЛЧАНОВА

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО ЧИСЛЕННЫМ МЕТОДАМ

Методические указания и задания для студентов математических специальностеи

Владивосток

Издательство Дальневосточного университета

2007

ББК 22.311 к 61

Рецензент:

Т.В. пак, к.ф.-м.н. (ИМКН ДВГ№);

г.,

к 61 Лабораторные работы по Численным методам. Учебно-методическое пособие. - Владивосток: Изд-во Дальневост. ун-та, 2007. - 36 с.

Лабораторные работы предназначены для студентов четвертого курса Института математики и компьютерных наук. Они поддерживают курс ^п Дополнительные главы математической физики ^и по следующим темам: методы коллокации, Ритца, Галеркина, конечных элементов для решения ОбЫКНОВеННЫХ дифференциальных уравнений, методы расщепления, приближенные методы решения интеграпьных уравнений. Пособие содержит варианты заданий и необходимый для их ВЫПОЛНеНИЯ теоретический материал. Для студентов математических специальностей.

1704020000

                                                                                 ББК 22.311

  Г., 2007 имкн ДВГУ, 2007

Содержание

1  Приближенные методы решения задач математической фи-

  зики                                                                                  4

1.1  Методы коллокации, Ритца, Галеркина, конечных элементов.    4

1.1.1  Метод коллокации5

1.1.2  Метод Ритца6

       1.1. З Метод Галеркина                                                                               9

      1.1.4 Метод конечных элементов                                             11

1.2  Методы сплайн-коллокации.       15

1.2.1  Г. Использование кубического сплайна           16

1.2.2  П. Использование В-сплайнов  18

2  Методы расщепления. Начально-краевая

  задача для двумерного уравнения теплопроводности.            20

З Решение интегрального уравнения

  Фредгольма 2 рода                                                                       21

  З. 1 Метод замены ядра на вырожденное                                         21

3.2  Метод Бубнова - Галеркина         24

3.3 

4  Варианты заданий           28

5  Литература           35

з

Известны различные подходы к конструированию РИНОСТНЫХ уравнений для задач математической физики. Особенно полно этот вопрос изу^Т-иеН дггя уравнений с коэффициентами, обладающими (вместе с решениями) достаточной гладкостью. В этом случае можно строить разностные схемы с высокой степенью аппроксимации. В ряде случаев представляется целесообразным получать приближенное решение с заданной точностью не за счет формального увеличения размерности подпространств (например, уменьшения шага сетки , а путем построения более точных аппроксимаций исходной задачи на основе априорной информации о гладкости решения. Такая точка зрения привела к удобным и достаточным универсальным методам построения разностных уравнении на основе вариационных методов Ритца, Галеркина, метода наименьших квадратов, метода КОНеЧНЬIХ элементов, методов СПЛаЙН-КОЛЛОКаЦИИ. В этих методах приближенное решение краевой задачи для дифференциального уравнения находится в виде аналитического выражения

1  Приближенные методы решения задач математической физики

1.1  Методы коллокации, Ритца, Галеркина, конечных элементов.

Дано дифференциальное уравнение и краевые условия в виде

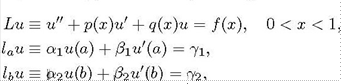(1)

(2)

где с ) - известные непрерывные функции, 01, 02, Д1,Д2, 71, 72 заданные постоянные, причем % 0 и 02! А- ,B21 0, р(с) > ро > 0,