Лабораторная
работа № 1
1
вариант.
Выполнил:
гр.
С8403б
Задача:
Методом Ритца решить краевую задачу
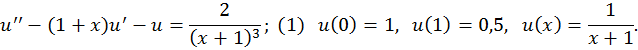
Решение.
Выберем базисные функции: 
.
Тогда получим
.
В качестве 
выберем
функции
удовлетворяющую краевым условиям задачи.
Ищем решение в виде суммы
В
исходном уравнении обозначим за P(x)
коэффициент при u', за Q(x)
- коэффициент при u и за F(x)
- правую часть. Тогда
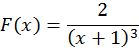
Следуя методу Ритца, введем замену
переменных:
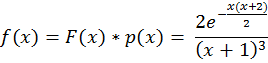
Тогда краевую задачу (1) можно свести к
задаче:
Краевая задача (3) равносильна минимизации
функционала:
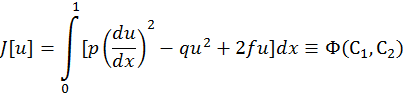
Общий вид функционала из-за его
громоздкости записывать не будем.
Далее найдем частные производные по С1
и С2 этого функционала. Расчеты произведены в математическом
пакете Mathcad Prime
2.0.
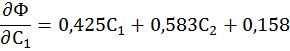
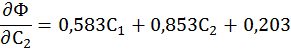
Приравнивая эти производные к нулю
получаем:
Подставляя найденные значения в (2)
получаем приближенное выражение для искомого решения:
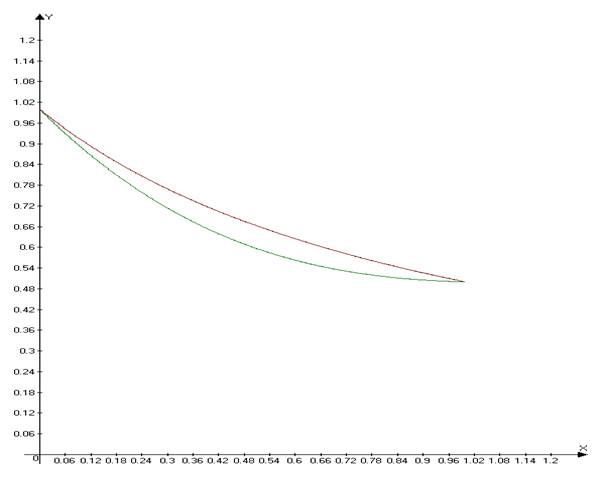
Построив графики точного решения 
(красный)
и полученного нами приближенного u(x)=
,
видим что на отрезке [0;1] они немного расходятся.
