обращалась в нуль на некоторой системе точек г1, с), ..., сп отрезка [а, Ь] называемых точками коллокации, причем число таких точек должно равняться числу коэффициентов Ci в выражении (4). Тогда для определения С1, С), Сп получаем систему уравнений
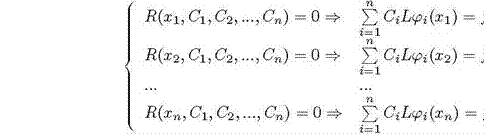 (7)
(7)
Решая эту систему относительно
коэффициентов Ci, находят решение в виде аналитического выражения (4)![]()
Пример 1. Методом коллокации решить краевую задачу
[1]![]()
![]() 1 = 0; и(—1)
1 = 0; и(—1)![]()
Решение. В качестве базисных функций выберем
полиномы Фо (с) ![]()
![]() (1 — т2к ), (К 1 2
...), которые удовлетворяют краевым условиям.
(1 — т2к ), (К 1 2
...), которые удовлетворяют краевым условиям.
![]() За точки коллокации возьмем со
За точки коллокации возьмем со ![]()
![]() Ограничиваясь тремя базисными
функциями, положим и = С1(1 -
Ограничиваясь тремя базисными
функциями, положим и = С1(1 -![]()
Подстановка в дифференциальное уравнение дает
R(c, СЧ, 02)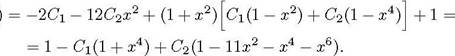
В точках коллокации имеем R(co) = 0, R(C1) 0. Отсюда, получаем для определения коэффициентов Ст и С) линейную систему уравнений
![]()
17 117
1 Ст
16
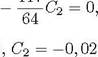
![]() решая которую находим (31 О 978
решая которую находим (31 О 978![]() 0 022. Приближенное решение имеет
вид
0 022. Приближенное решение имеет
вид
![]()
![]() и о, 978(1 - Р) - о, 0216с2 (1
и о, 978(1 - Р) - о, 0216с2 (1![]() с4 ) о, 9564 — о, 978х 2 + о, 0216х4
.
с4 ) о, 9564 — о, 978х 2 + о, 0216х4
.
![]() 1.1.2 Метод Ритца
1.1.2 Метод Ритца
В уравнении (1) предполагается, что оператор L является симметричным L L* и положительно-определенным линейным оператором в гильбертовом пространстве Н. Тогда краевая задача (1) равносильная задаче о
минимизации функционала
|
Щи]
|
(Lu, и) — 2(f, и). |
(8) |
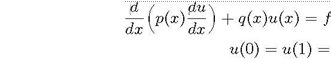
этот функционал имеет вид
1
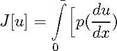 2 qu2 А- 2fu dc. (10)
2 qu2 А- 2fu dc. (10)
В общем случае линейное дифференциальное уравнение![]()
![]()
можно записать в самосопряженном виде (9), если ввести
замену перемен![]() ных
ных
![]() >
0, ч (с)
>
0, ч (с) ![]() f(c)
f(c)![]()
Решение задачи (1)-(3) ищем в виде (4). Подставляя
выражение (4) в формулу (10), получаем щи]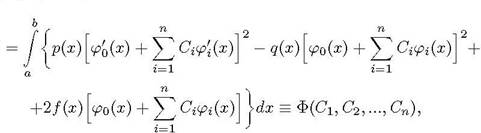
![]() где Ф(С1, С),
сп) - квадратичная функция переменных Ст, (32, сп . Для того, чтобы
дифференцируемая функция Ф(С1 С), , сп) при некоторых значениях С1, ..., Сп
имела экстремум, необходимо соблюдение для этих значений следующий условий:
где Ф(С1, С),
сп) - квадратичная функция переменных Ст, (32, сп . Для того, чтобы
дифференцируемая функция Ф(С1 С), , сп) при некоторых значениях С1, ..., Сп
имела экстремум, необходимо соблюдение для этих значений следующий условий:
![]() 1 п, (11)
1 п, (11)![]()
где
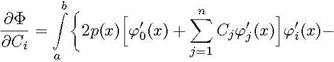
![]() 2q(c) [ро (с) + Сјрј (с)ј (с) 2f
(с) А (с)
2q(c) [ро (с) + Сјрј (с)ј (с) 2f
(с) А (с)![]()
Система (11) является линейной
относительно коэффициентов сг, С), ![]() сп , причем число уравнений равно
числу неизвестных. Решив ее, най
сп , причем число уравнений равно
числу неизвестных. Решив ее, най![]() дем коэффициенты Ci(i 1, п), что
позволяет затем записать решение в виде (4)
дем коэффициенты Ci(i 1, п), что
позволяет затем записать решение в виде (4)![]()
Пример 2. Методом Ритца решить краевую задачу [1]![]()
![]() И. (1 с 2 и 1
= 0; и(—1)
И. (1 с 2 и 1
= 0; и(—1)![]()
Решение. В качестве базисных функций выберем полиномы ро (с) 0
![]() (1 Т2К) (К = 1,2, которые
удовлетворяют краевым условиям
(1 Т2К) (К = 1,2, которые
удовлетворяют краевым условиям
Ограничиваясь тремя базисными функциями, ищем решение
в виде суммы и = С1(1 ![]() Данное уравнение, где
Данное уравнение, где
Р(с)
1 q(c) ![]()
является самосопряженным. Составляем для него соответствующий функЦИОН2Л
1 щи]![]()
—1
![]() Заменяя и его
выражением и (31 (1 — с 2 ) С2(1 получаем
Заменяя и его
выражением и (31 (1 — с 2 ) С2(1 получаем
1![]()
![]()
—1
Частные производные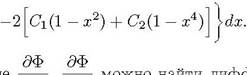 можно найти
дифференцированием индсг' да теграла Щи] по параметрам СГ и С):
можно найти
дифференцированием индсг' да теграла Щи] по параметрам СГ и С):
1 ![]()
![]()
![]() 4с(2СIС
4с(2СIС ![]() + с — с) ) [Ст (1 c 2 )-FC2 (1 — г 4 дсч
+ с — с) ) [Ст (1 c 2 )-FC2 (1 — г 4 дсч![]()
—1 ![]()
1
![]() 8х 2 (2 Ср 4c2c 3 )
2(1
8х 2 (2 Ср 4c2c 3 )
2(1 ![]()
—1![]()
![]()
Приравнивая эти производные нулю, получаем систему уравнений

откуда находим, что сг 0 988 С) —0 054. Подставляя найденные значения в формулу (4), получаем приближенное выражение для искомого решения
![]()
![]()
![]() О,
О,
934 - О,0, 054х4
1.1. З Метод Галеркина
В методе Галеркина не требуется самосопряженность оператора
L. Реше![]() НИе ищется в виде (4) и согласно
этому методу невязка R Lu,n — .f должна быть ортогональна ко всем базисным
функциям.
НИе ищется в виде (4) и согласно
этому методу невязка R Lu,n — .f должна быть ортогональна ко всем базисным
функциям.
Запишем условие ортогональности
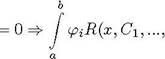 cn)dc
cn)dc где
![]()
Тогда для определения коэффициентов Сё имеем систему линейных алгебраических уравнений
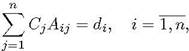 (12)
(12)
где
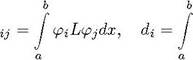 pz (с) — Про dc
pz (с) — Про dc![]()
![]()
Пример З. Методом Галеркина решить краевую задачу
[1]![]()
![]() И. (1 с 2 и 1
= 0; и(—1)
И. (1 с 2 и 1
= 0; и(—1)![]()
Решение. В качестве базисных функций выберем
полиномы ро (с) 0![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.