Приближенные методы решения задач математической физики. Методы коллокации, Ритца, Галеркина, конечных элементов, страница 3

(1 Т2К) (К = 1, 2, ...), которые удовлетворяют краевым условиям

Ограничиваясь тремя базисными функциями, ищем решение в виде суммы и = С1(1 -

Подставляя и в левую часть дифференциального уравнения, получаем невязку

R(c, С1,С2) С1(-2) С2(-12с ² )1.

Условие ОРТОГОН&ПЬНОСТИ функции R(c, С1, С) ) к функциям 91 (с) приводят к системе

      1                                              1

        (1 -                   СЧ, C2)dc О,                 (1 -  сг, C2)dc О.

        —1                                                                         —1

Подставляя вместо R(c, Ст, С) ) его значение, после соответствующего интегрирования получаем систему

1

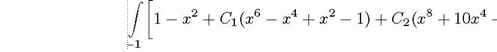
4  152            16

(32      0 з              1059          

1

    10х6      4 11 с2     1) dc

—1

0.

5  9

Решая систему

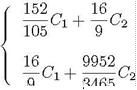4

З

8

5 находим (71 0, 988, С)   —0 0543 и следовательно,

     ) 0, 0543(1 — с ⁴) о, 9334 - о, 988х²             о, 0543х⁴

1.1.4 Метод конечных элементов

Основной идеей новых методов построения разностных схем на основе ваРИ&ЦИОННЫХ принципов является использование функций с конечными носителями, т.е. функций, которые в сравнительно небольшой (порядка шага сетки) окрестности отличны от нуля, а вне ее тождественно равны нулю. Решение искомой задачи (1) ищется в виде линейной комбинации функций с конечным носителем при неизвестных коэффициентах, которые выбираются на основе минимизации того или иного функционала, связанного с вариационной постановкой задачи.

Дано дифференциальное уравнение и краевые условия в виде

Lu(13)

и(а) — 0, u(b) = 0(14)

Введем на отрезке [а,Ьј равномерную сетку с шагом hсостоящую из п внутренних точек (узлов) гт• а + ih (i12, ... , п) и двух крайних узлов - со а, сп+1

Применим метод Галеркина для решения задачи (13) - (14), в котором функции А (с) задаются равенствами

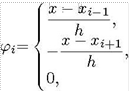если с €- [с— 1, если С [Ci,Ci+1], если с         Ti_1, Ci+1].

Данные функции линейно независимы, ортогональны и образуют полную систему в пространстве L2[a, Ь]. Это дает основание для их законного применения в качестве базисных функций метода Галеркина.

Приближенное решение ищем в виде

                                                                 (16)

Для подсчета коэффициентов Ci согласно методу Галеркина, нужно составить линейную алгебраическую систему (12). Ее правые части в таком случае суть

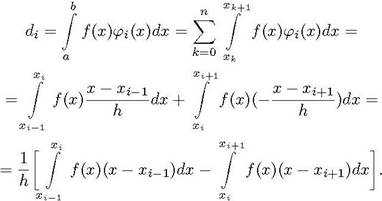                         (17)

Так как при краевых условиях (14) используются п базисных функций с 91 по рп, и все они в точках а и Ь равны нулю, то формула для вычисления коэффициентов Aij линейной алгебраической системы уравнений имеет вид

         (18)

В силу отмеченного выше неравенства нулю на элементарном промежутке лишь соседних по индексу ФИНИТНЫХ функций и их производных, можно считать отличными от нуля фигурирующие в выражении Aij произведения р; (с)р; р? (с)рј (с), рј только в тех случаях, когда i—1<j<i 1. Это означает, что

Aij = 0 при z—jl > 1(19)

т.е. матрица А (Aij) системы (12) является треугольной матрицей. Это позволяет применять для ее решения метод ПРОГОНКИ.

Конкретизируем формулы для вычисления ненулевых элементов матрицы А. Полагая в (18) .ј i, с помощью выражения (15 получаем формулы для вычисления диагональных элементов:

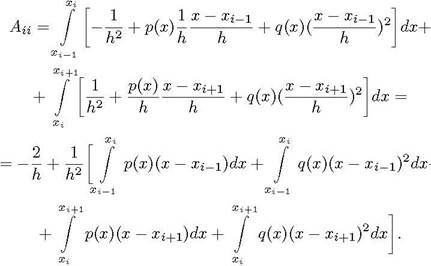                  (20)

При j=i 1 из (18) находим выражение элементов правой побочной диагонали матрицы А:

а при

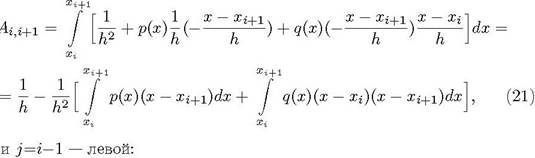
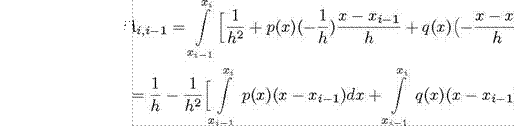(22)

Замечание. При неоднородных краевых условиях первого рода

                       и(а) 71, u(b) 72                                                   (23)

можно свести задачу (13), (23) к задаче

где

Р (с) f(c) —                                                           (с) —72 71(г а), Ь         а

с однородными условиями

                    ш(а) 0, ш (Ь)       0

Найдя методом конечных элементов приближенное решение

                  (Шп(с)         CiPi(c), получаем и(с) ип(с) wn(c)

Пример 4. Методом КОНеЧНЫХ элементов решить краевую задачу [1]

+ (1 + г2)и+1 О; и(—1)

    Решение. Вводим на отрезке [-1,1] равномерную сетку                ih с шагом