Приближенные методы решения задач математической физики. Методы коллокации, Ритца, Галеркина, конечных элементов, страница 7

У2(с) = (71 • 1 с2с + Сзс ²

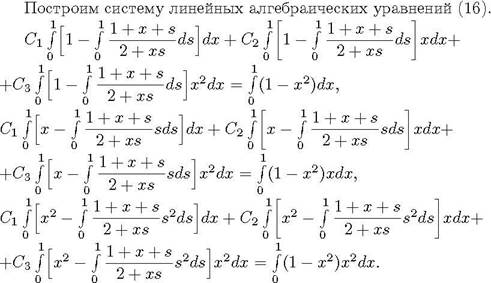
Подсчитав интегралы, получим систему уравнений относительно неизвестных коэффициентов:

             о, 0,019003     2/3, о, 0386С1 +0, 0957С2 + о, 089403 1/4, о, +0, 089402+ 0 0918С3 2/15

Решая данную систему, получим (31 = 5, 2785, С)      1,6292, сз         1, 2267 или

             92 (с)    5,           1,          - 1,2267х ²

4 BapnaHTb1 3aĄaHMił

Ta6J11Ąqa 1, BapnaHTb1 38JĄa.H K ^rreMa,M I 2

2	1,
	2T.e
(T 2 I) u — 2Tt_l, u(o) 2d(o) — 1, u(l) — O, 5; 1 1	4, 5 (T 1)B/2 ; u(o)2/2,
3u(0)	10. u
Il.u 3u(0)	0, 5u             1 12. t/' + 3u(0)      2u'(0) — 1; u'(l) — 2;        2                              1 (T + l)B/2 +
13.u'	1,
u z: 3 sin T — cos T,' (cos 1+3 sin 1); sm T.	—2—3/2.
		20.u
		22. u"
		24.
		26. d'	(sin   COS T)' 1; u(l) + u'(l) 2 sin 1, sin — cos C.
		27. u u(0)	0, 5 sin cos 1— sin 1;
29. u(0) — O; u'(l) = 3/4; 2

BapnaHTb1 Me^rr0AOB pacruer1JueHþ1¶

1. 1-1eflBHûJfl cxeMa FlepeMeHHB1x Ha,L1paBJ1eHLff (Elp0A0J1bH0 - F10L1epeHHûJfl

O, 57

0+1/2

o, 12,

9.  Λι υ ^π+ ¹ / ² ΛΙ υ ^η Η- 2Λ2υ ^π + φ ^η ,

0, 57

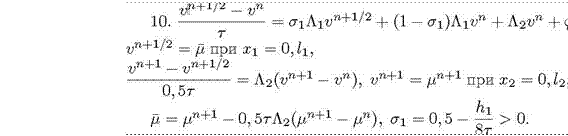
11

0, 57 ηΗ_1         η+1/2

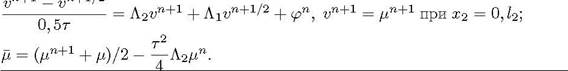
0, 57

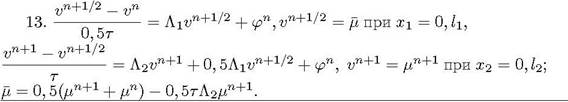
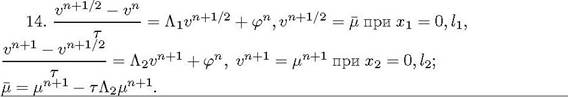
 μ ^η+ ¹      12 h2

μ

0, 5 μη+1

σισ2τΛ2μη+ 1 +0, 5/-ιη + 0,

—

(72

0, 5

(E — —TA2)Vn+1

1 25  f (2x — s)u(s)ds	6	FarlepKHH
2 Tr 26  sin cos su (s) ds	cos 2x	FaunePKHE-1
1 27 S u (s)ds e		FaunePKHE-1
1 28		FaunepKHH
29 sin(œ s)u(s)ds	cos	FanepKHH

5 Литература

1.  Демидович Б.П., Марон И.А., Шувалова ЭВ. Численные методы анализа.            ФМ, 1962.

2.  Вержбицкий. Основы численных методов.            Высшая школа, 2002.

3.  Верлань А.Ф. Интегральные уравнения. -Киев: Наукова думка, 1986.

4. Завьялов Ю.С., Квасов Б. И., Мирошниченко В.Л. Методы сплайнфункций. Наука, 1980

5. Колобов А.Г. Метод сплайн-коллокации. Методические указания. - Владивосток, ДВГУ, 1998

6. Колобов А. Г. Сплайн-функции. Методическое пособие. - Владивосток, ДВГУ, 1999

7.  Копченова НВ. Марон И. А Вычислительная математика в примерах и задачах. -М.: Наука, 1972.

8.  Краснов М. Л., Макаренко Г.И., Киселев А.И. Вариационное исчисление. Наука, 1973.

9.  Краснов М.Л., Киселев А.И., Макаренко Г. И. Интегральные уравнения.

Наука, 1968

10.  Марчук Г. И. Методы вычислительной математики. -М.: Наука, 1980.

11.  Самарский А. А. Введение в теорию ралЗНОстных схем. -М: Наука, 1971

12.  Самарский А. А., Гулин А. В. Численные методы. -М.: Наука, 1989.