![]() Пример 1. Методом замены
ядра на вырожденное найти решение уравнения
Пример 1. Методом замены
ядра на вырожденное найти решение уравнения
1
![]()
Решение. Ядро уравнения К (с, s) С (ecs 1) аппроксимируем суммой трех членов разложения К (с, s) в ряд Тейлора, т.е. положим
![]() (8)
(8)
2 6
Тогда решение уравнения (1) будем искать в виде
![]() с + Ст с2 + ас з А- Сзс
с + Ст с2 + ас з А- Сзс![]()
Обозначая с), 02 с з, 03 с , F1(s) ![]()
![]() S 3 /6, .f(T) г,
находим по формулам (6) коэффициенты системы
S 3 /6, .f(T) г,
находим по формулам (6) коэффициенты системы
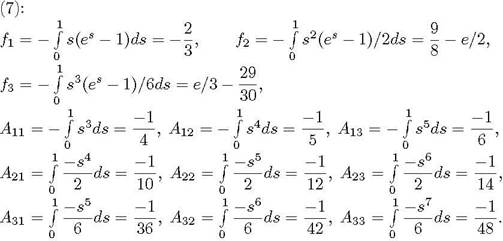
Таким образом, имеем систему
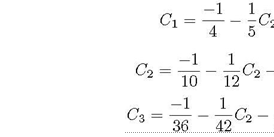
Ее можно преобразовать к виду:![]()
Решая ее, получим 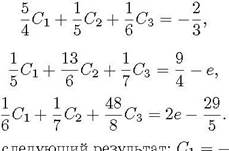 следующий
результат: Ст 0,5010, съ о, 1671,
следующий
результат: Ст 0,5010, съ о, 1671, ![]() —0 0422. Следовательно,
приближенное решение уравнения (1) можно записать в виде
—0 0422. Следовательно,
приближенное решение уравнения (1) можно записать в виде
![]()
Уз
(с) с— 0, 5010х о, 1671х![]()
Точное решение интегрального уравнения: у(с) 1. Из найденного приближенного решения при с 0 5; 1 имеем
![]() 1, 0000, z(0, 5) 1, 0000, z(1) 1, 0080
1, 0000, z(0, 5) 1, 0000, z(1) 1, 0080
![]()
т.е. расхождение с точным решением всего 0,008.
3.2 Метод
Бубнова - Галеркина![]()
Приближенное решение интегрального уравнения
и (с) .f(T) ![]() А К (с, s)u(s)ds
А К (с, s)u(s)ds
по методу Бубнова - Галеркина ищется так. Выбираем систему линейнонезависимых функций {рп(с)}, полную в L2(a, Ь) и ищем приближенное решение ив (с) в виде
![]() Скрк
Скрк ![]() к-=1
к-=1
![]() Подставляя (с) в интегральное
уравнение, получаем невязку в следующем виде
Подставляя (с) в интегральное
уравнение, получаем невязку в следующем виде
![]()
![]() Скрк (г) — .f(T,)
Скрк (г) — .f(T,)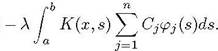
Коэффициенты СК находятся из условия
ОРТОГОН&ПЬНОСТИ невязки R ко всем базисным функциям:![]()
(R,Pi) - 0,![]()
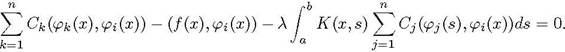
Коэффициенты ск (К 1, 2, ..., п) определяются из следующей линейной системы

(К = 1,2, п![]()
Пример 2. Методом Бубнова-Гиеркина найти решение уравнения
1
ф)![]() u(s)ds 1 — с 2 . (9)
u(s)ds 1 — с 2 . (9)
Решение. В качестве полной системы функций на отрезке [0,1] выберем систему А (с)
с и . Приближенное решение уравнения (1) будем искать в виде![]()
![]()
Подставляя (с) вместо и(с) в уравнение (9), будем иметь невязку
1
![]()
![]()
![]()
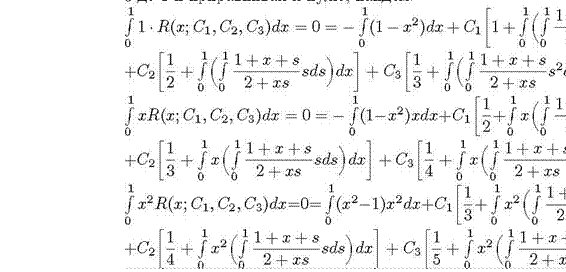
Подсчитав интегралы, получим систему уравнений относительно неизвестных коэффициентов:
о, 1188С1 о, 038632![]()
|
о, 038601 о, 095702 |
|
1/4 |
|
|
|
О, 0918Сз |
2/15. |
|
|
Решая данную систему,
получим сг |
|
1 6292, сз |
1 2267 |
У2 (с) 5 2785![]()
З .З Метод Ритца.
С помощью метода Ритца реализуется вариационный подход к построению приближенно-аналитического решения интегрального уравнения
Данному уравнению сопоставляется функционал
Щи] (Lu, и) —
2(f, и)![]()
для которого ищется решение экстремальной задачи
![]()
Взаимно однозначное соответствие между решениями
задачи (12) с Щи] вида (11) и задачи (10) имеет место при условии
симметричности и положительной определенности оператора [3]![]()
![]() По методу Ритца приближенное
решение вариационной задачи (12) ищется в виде
По методу Ритца приближенное
решение вариационной задачи (12) ищется в виде
![]()
![]()
![]() Е, CiPi, где Ci (i 1 2 п) - неизвестные коэффициенты, а
Е, CiPi, где Ci (i 1 2 п) - неизвестные коэффициенты, а ![]() - система линейно независимых и
полных базисных функций.
- система линейно независимых и
полных базисных функций.
Задача минимизации функционала (12) сводится к задаче минимизации функции п переменных
![]() = (L E ci9i ,E Ci9i)
= (L E ci9i ,E Ci9i)
 ( 14)
( 14)
которая заменяется равносильной задачей решения СЛАУ
C1(L91,
91) + C2(L91, 92)![]() Cn(L91, = (91, Л,
Cn(L91, = (91, Л,
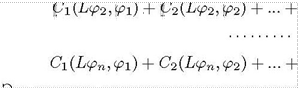 Cn(L92, Ра) =
(92, Л,
Cn(L92, Ра) =
(92, Л,
Спфрп,рп)![]()
Эта система получается приравниванием к нулю производных
![]() ДФ(С1, ..., сп)
ДФ(С1, ..., сп)
В случае интегрального уравнения (10) эта система имеет вид
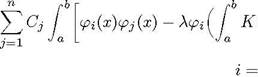 К (с, s)pj
(s)ds) А (с) dc
К (с, s)pj
(s)ds) А (с) dc ![]() (c)dc,
(c)dc,
Пример З. Методом Ритца найти решение уравнения
1
![]() (17)
(17)
Решение. В качестве полной системы
функций на отрезке [0,1] выберем систему (с) с и Приближенное
решение (с) уравнения (17) будем искать в виде![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.