Приближенные методы решения задач математической физики. Методы коллокации, Ритца, Галеркина, конечных элементов, страница 5

 01ho + 3/31,

 271 (2ho Н— h1)'

Уравнения (12), (14) образуют систему п З уравнений относительно ПА- З неизвестных Л.. Исключив с помощью уравнений (14) неизвестные b1 и Ьп+1 из (12), приходим к системе с трехдиагониьной матрицей

          Ь К _1АК + Ь К СК bk+1Dk = Fk К = 1,71-1,                 (15)

где со - С_1Ао/А_

- D_1Ao/A_ сп = сп - Cn+1Dn/Dn+1, - F_1Ao/A_ = р; - Fn+1Dn/Dn+1.

В итоге реализация метода сплайн-коллокации сводится к вычислению коэффициентов bo, , Ьп из системы (15) (с помощью метода прогонки) и определению b_1, Ьп+1 из уравнений (14)

Пример 2. С использованием В-сплайнов решить краевую задачу [1].

Решение. Вводим на отрезке [-1,1] равномерную сетку ск с шагом 0, 5 и дополняем ее двумя узлами в начале и конце построеннои сетки

Ищем решение в виде разложения по базису из нормализованных кубических В-сплайнов:

Ь2В2(с) b5B5(c).

Находим по формулам (13) и (16) коэффициенты системы уравнений

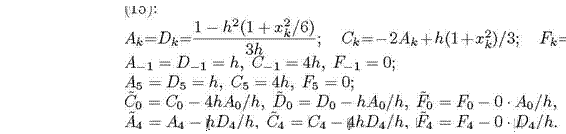
Система имеет вид:

s(0) ЛИ (-0, 5) b2B(0) Ь (0, 5) 7336/6 о, 2/3 892; S(0, b3B(0, 97+0, 0417)/6+0, 7336 * 2/3=0, 6577 S(1) = = О, 9002/6 = О.

2 Методы расщепления. Начально-краевая задача для двумерного уравнения теплопроводности .

На плоскости с г1, с) ) рассмотрим область G с границей Г [11, 12] Будем искать решение задачи теплопроводности в области (З = G Г для всех 0 < t < Т. Требуется найти функцию и(с, t), определенную в цилиндре G х [0, Т] {(c,t) : с О, 0 < Т}, удовлетворяющую в QT с, t) : с G, О < t < ТУ уравнению теплопроводности

д2и

                           (L1 +L2)u,           (1)

краевым условиям первого рода на границе Г области (З

и = „(г“), саг,

и начальному условию при t 0:

Предположим, что G - прямоугольник со сторонами [1 и Ь:

Введем в G прямоугольную сетку

i2h2),1, 2}

с границей

(i1h1, i2h2),

Оператора заменим разностным оператором Ла:

л = Л1+Л2.

Используя заданное точное решение, построить начально-краевую задачу для уравнения теплопроводности и затем решить одним из указанных ниже методов. Пространственные переменные меняются на отрезке [0,1] . Шаги по пространству берутся равным 0,1. Варианты точных решений:

1, И tec+y.

2. и = tsinrc sin ту; 2.

4, и t О, 25(с ² + у ² ).

З Решение интегрального уравнения Фредгольма 2 рода

Рассмотрим интегральное уравнение Фредгольма второго рода

               и (с) — А К (с, s)u(s)ds      f(c)                              (1)

Для нахождения приближенного решения этого уравнения будем использовать три метода: метод замены ядра на вырожденное, метод Галеркина и метод Ритца

З. 1 Метод замены ядра на вырожденное

Ядро К (с, s) называется вырожденным, если оно представимо в виде

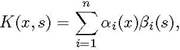                                                               (2)

где функции с и  1, п) линейно независимы на отрезке [a,b].

Предлагаемый метод основан на том, что для интегрального уравнения (1) с вырожденным ядром может быть получено точное решение. Заменим приближенно ядро К (с, s) вырожденным

и будем искать приближенное решение уравнения (1) в виде

где

                                                                     (5)

Подставляя выражение (4) в (5), получим

         (s)f (s)ds + А 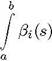С, аз (s)ds (2        1,2      п).

Вводя обозначения

             (s)f (s)ds                    (6)

будем иметь

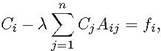                                                                       (7)

Получаем систему ЛИНеЙНЫХ алгебраических уравнений ОТНОСИТ&пЬНО Ci. Решив эту систему, записываем приближенное решение уравнения (1) в виде (4). В качестве вырожденного ядра можно взять отрезок рада Тейлора или ряда Фурье для функции К (с, s).