При изучении случайных явлений часто приходится иметь дело с несколькими случайными величинами. Совокупность с.в. Х и Y, рассматриваемых совместно, называется системой двух случайных величин (или двумерной случайной величиной) и обозначается (Х, Y). Например, точка попадания снаряда характеризуется системой (Х, Y) двух случайных величин – абсциссой Х и ординатой Y.
Функцией распределения F x y( , )системы (Х, Y) называют функцию, ставящую в соответствие каждой паре вещественных чисел (x y, ) вероятность совместного выполнения неравенств X < x, Y < y , т.е.
F x y( , ) = P X( < x Y, < y) (1)
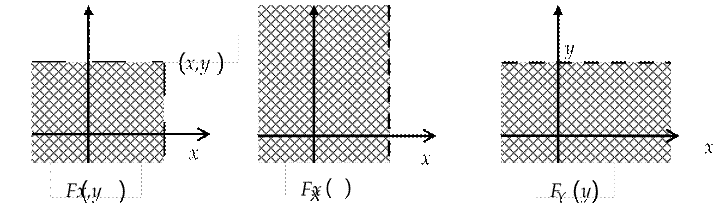
Геометрическифункция распределения имеет смысл вероятности попадания случайной точки (Х,Y) в бесконечный квадрант с вершиной в точке (x y, ), лежащий левее и ниже её.
При этом легко найти функции распределения каждой из с.в., входящих в систему (X,Y). Для св Х. . : FX (x) = P X( < x) = P X( < x Y, < ∞) = limy→∞ F x y( , ).
Для св. . Y : FY ( )y = P Y( < y) = P X( < ∞,Y < y) = limx→∞ F x y( , ).
Геометрическая интерпретация: F x y( , ), FX (x), FY (y) – это вероятности попадания случайной точки в соответствующие заштрихованные области (см. рисунок).
y y
y
Основные свойства функции распределения системы двух с.в. аналогичны свойствам функции распределения одной с.в.:
1. 0 ≤ F x y( , ) ≤ 1.
2. F x y( , ) −неубывающая функция по каждому из аргументов т е, . .
при x2 > x1 F x( 2,y) ≥ F x( 1,y); при y2 > y1 F x y( , 2) ≥ F x y( , 1).
3. F x( ,− ∞) = F (−∞, y) = F (−∞ − ∞, ) = 0.
4. F x( ,∞ =) FX ( )x , F (∞, y) = FY ( )y .
5. F (∞ ∞ =, ) 1.
Для системы непрерывных с. в. рассматривают плотность вероятности
.
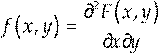
(2)
Её свойства:
1. f x y( , ) ≥ 0
∞ ∞
2. ∫ ∫ f x y dxdy( , ) = 1.
−∞−∞
Функция распределения выражается через плотность вероятности по формуле: x y
F x y( , )= ∫ ∫ f s t dsdt( , ) .
−∞−∞
Матрицей распределения системы ДСВ (X Y, ) называют таблицу, в которой перечислены все возможные значения xi с.в. X (i = 1,2,...,n), все возможные значения yj с.в.
Y ( j = 1,2,...,m) , а также вероятности pi j = P X( = x Yi , = y j ).
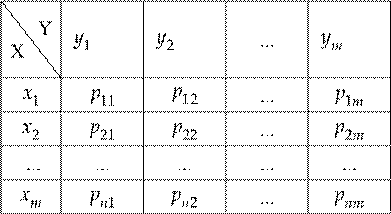
Зная матрицу распределения, можно составить ряды распределения для X и Y. Например, ряд распределения с.в. X:
|
xi |
x1 |
x2 |
... |
xn |
|
pi |
p1 |
p2 |
... |
pn |
m n m
Здесь pi = P(ξ= xi ) = ∑pi j , ∑∑pi j = 1.
j=1 i= =1 j 1
Условные законы распределения. Независимость с.в.
Условным законом распределения с.в. Y, входящей в систему (X Y, ), называют закон её распределения, вычисленный при условии, что с.в. Х приняла определённое фиксированное значение.
Для системы дискретных с.в., заданной приведённой выше матрицей распределения, pi j − вероятность совместного выполнения равенств (X = xi ) и (Y = y j ), т.о. pi j − это вероятность произведения событий A ={X = xi} и B ={Y = y j}:
pi j =P X x Y y(
=
i ,
=
j )
=P AB(
) =P A P B A(
) (
) =P B P AB(
) ()
. Отсюда получаем P AB(
) = P AB(
) ,
P B( )
()
P X x Y y(
=
i ,
=
j ) pi j
, (3)
P X x Y y= i= j = = n P Y y( = j ) ∑pi j
i=1
аналогично P
BA( ) = P
AB( ) , P
A(
)
P Y y X x(
=
j=
i )
=
P X x Y y(
P X x=(
i=, i=)
j ) ∑pi jpi j .
(4)
= m
j=1
Вероятности, найденные по формулам (3) или (4), образуют условные ряды распределения, при условии, что, соответственно, Y = y j или X = xi . Как и для любого ряда распределения сумма этих вероятностей равна единице:
nm
∑P
X( = x Yi = y j )
=
∑
P Y( =
y j 
X = xi)
= 1.
i=1 j=1
Для системы непрерывных с.в. (X Y, ) вводится условная плотность вероятности. Обозначим
fX (x
y)
= ff(Y x y(
),y )
= ∞∫
ff ((x y dxx y,,
))
(5)
−∞
условную плотность вероятности Х при условии, что Y = y ; предполагается, что знаменатель отличен от нуля. Аналогично
fY ( y x) = ff(Xx y(
),x )
= ∞∫
ff ((x y dyx y,,
)) .
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.