Системы случайных величин. Понятие о предельных теоремах теории вероятностей, страница 6

xi	0	1	2	3	4	5
ni	1	2	1	1	2	3

Решение. а) Ранжируя исходный ряд, получим вариационный ряд: 0, 1, 1, 2, 3, 4, 4, 5, 5, 5. б) Вычислив частоту и частость вариантов x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3,x₅ = 4, x₆ = 5 , получим статистическое распределение выборки – так называемый дискретный статистический ряд:  6

,     ∑n_i = 10,

i=1

или

xi	0	1	2	3	4	5
pi∗	0.1	0.2	0.1	0.1	0.2	0.3

6

,      ∑pi∗ = 1.

i=1

Статистическое распределение выборки служит оценкой неизвестного закона распределения с.в. Х и при большом объёме выборки n мало отличается от истинного.

            Если число значений изучаемого признака (с.в. Х) велико или признак является непрерывным (т.е. с.в. Х может принять любое значение в некотором интервале), составляют интервальный статистический ряд. В первую строку таблицы статистического распределения вписывают частичные промежутки ^^x₀,^x₁), ^^x₁,^x₂ ), ...^^x_k−1,^x_k ), которые берут обычно одинаковыми по длине: h = x₁ − x₀ = x₂ − x₁ = ... = x_k − x_k−1 .  Для определения величины интервала h можно использовать формулу Стерджеса: h ⁼ (x_max − x_min )/m , , где x_max − x_min – разность между наибольшим и наименьшим значениями признака, m – количество интервалов, m = 1+ log₂ n ≈ 1+ 3.322lgn . За начало первого интервала принимают x_нач = x_min − h/ 2 .            

Во второй строчке интервального статистического ряда записывают количество наблюдений n_i (i = 1, 2, ..., k), попавших в каждый интервал.

Пример 3. Измерили рост (с точностью до см ) 30 наудачу отобранных студентов. Результаты измерений таковы:    

178,160,154,183,155,153,167,186,163,155,157,175,170,166,159,173,182,167,171,169,

179,165,156,179,158,171,175,173,164,172.

Построитьинтервальный статистический ряд.

Решение. Проранжируем полученные данные:  

153,154,155,155,156,157,158,159,160,163,164,165,166,167,167,169,170,171,171,172,

173,173,175,175,178,179,179,182,183,186.

Как видим, ^x_max = 186, ^x_min = 153; по формуле Стерджеса, при объёме выборки n = 30, находим длину h частичного интервала 

h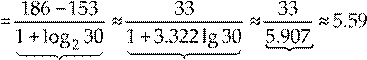 . Примем h = 6. Тогда x_нач = 153−  = 150 ,

m m         m m ≈ 6 . Исходные данные разбиваем на m = 6 интервалов:

[150,156 , 156,162 , 162,168 , 168,174 , 174,180) [ ) [ ) [ ) [ ),[180,186). Подсчитав число студентов (n_i ), попавших в каждый из полученных промежутков, получим интервальный статистический ряд:

Рост	[150,156)	[156,162)	[162,168)	[168,174)	[174,180)	[180,186)
Частота ni	4	5	6	7	5	3
Частость pi∗	= 0.13	= 0.17	= 0.20	= 0.23	= 0.17	= 0.10

            Эмпирическая (выборочная) функция распределения

Эмпирической (выборочной) функцией распределения для выборки объёма n называется функция F_n^∗( )x , равная для каждого x относительной частоте (частости) события

{X < x}:                      F_n^∗( )x = n_x /n ,

где n_x – число наблюдений, меньших x, x∈ −∞ +∞(   ,  ).

При увеличении числа n наблюдений относительная частота события {X < x} приближается к его вероятности. Эмпирическая (выборочная) функция распределения F_n^∗( )x служит оценкой вероятности события {X < x}, т.е оценкой теоретической функции распределения F x( ) с.в. Х.

Пример 4. Построить функцию F_n^∗( )x , используя условие и результаты примера 2. 

Решение. Здесь n = 10. При x F                          x         .к. нет вариантов, меньших нуля.

При .к. здесь n_x = 1 и т.д. Окончательно получаем

                                                            График этой функции приведён на рисунке.

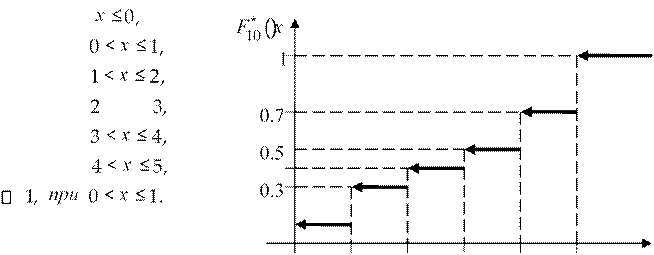
 0, при



_0.1, при 0.3, при



F      x        0.4,



_0.5, при 0.7, при



    0          1         2          3         4          5            х