Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов

1. ЦЕЛЬ РАБОТЫ        

Целью работы является изучение принципов кодирования и декодирования циклических кодов, а также знакомство с техническими методами  и устройствами, реализующими эти принципы.

2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Циклические коды - наиболее распространенный тип избыточных  кодов,    используемый для повышения достоверности передачи дискретной информации, по линиям связи. Циклические коды имеют блочную структуру и относятся к систематическим разделимым кодам. Каждый блок передаваемой информации состоит из информационной и проверочной части. Проверочные символы блока являются линейной комбинацией информационных символов того же блока. Число элементов в блоке (n) в информационной (k) и проверочной (n-k) частях фиксировано и известно заранее. Наличие проверочной части позволяет на приемной стороне линии связи обнаружить ошибку и даже исправить ее.        

Пусть , i={1,2…,k} ; , j = {1,…,n-k} - соответственно символы информационной и проверочной частей блока. Тогда кодовая комбинация  систематическою кода может быть  представлена в виде:

 ;
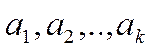
где 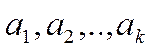 ; - информационная часть,    -  проверочная часть. Проверочный символ  определяется линейным соотношением

   ;

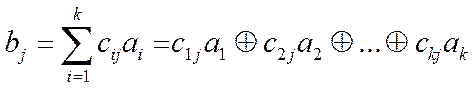здесь знак  означает сложение по модулю два;

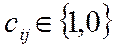 - производящий вектор для j-го проверочного символа. Для полного определения систематического кода необходимо располагать (n-k) производящими векторами, образующими производящую матрицу 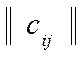 Каждая строка этой матрицы есть соответствующий производящий вектор.

Производящая матрица циклического кода обладает дополнительным свойством: все строки этой матрицы могут быть получены циклическим сдвигом одной, называемой образующей данного кода.

Основная проблема при разработке экономичных и удобных для реализации методов кодирования - нахождение производящей матрицы или образующего кода. Решение этой задачи требует знания специальной алгебраической теории кодирования. Некоторые сведения из этой теории приводятся ниже.

2 1. Основные понятия и определения алгебраической теории кодирования

1. n-разрядные комбинации циклического кода представляются в виде многочлена фиктивной переменной  x:

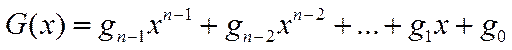
В случае двоичного кода коэффициенты этого полинома могут принимать только два значения: 0 и 1. В такой записи, например, восьмиэлементная комбинация 10011101 представляется в виде полинома 7-й степени:

.

Таким образом, многочлен G(x) – это условная форма представления кодограмм, в которой все символы кода представлены коэффициентами многочлена, причем старшим символам кода соответствуют старшие коэффициенты многочлена.

2. Многочлены можно складывать делить и умножать по определенным правилам.

Пусть 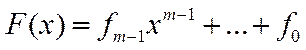   некоторый многочлен степени m-1.

Сложение  многочленов G(x) и F(x) осуществляется по обычным правилам сложения  алгебраических многочленов, однако подобные члены приводятся по модулю два.

Деление  многочлена G(x) на  F(x) определяется алгоритмом Эвклида

;

где h(x) – частное от деления ;  r(x) –остаток.

Простое произведение многочленов    находится по обычным правилам умножения алгебраических многочленов с приведением подобных членов по модулю.

Произведение двух многочленов G(x)  и  F(x) по модулю полинома P(x)  -  это остаток r(х) от деления произведения G(x)F(x) на полином Р(x) Символически эта операция обозначается так:

 ;

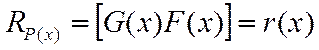k-й степенью многочлена G(x) по модулю полинома  Р(x) называется  остаток oт деления k-кратного простого произведении G( x )G(x)…на полином P(x):

;

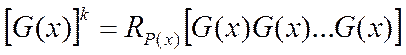3.Полином Р(х) называется неприводимым, если разложение его  на множители вида  невозможно  в классе многочленов с коэффициентами 0 и 1. Другими словами,  Р(х) является неприводимым, если уравнение Р(x) = 0 не имеет корней, равных 0 или 1.

4. Множество многочленов степени не выше n-1 называется конечным полем или полем Галуа.  Поле многочленов замкнуто относительно операции сложения и умножения по модулю неприводимого многочлена в том смысле, что применение упомянутых операций к двум элементам поля дает результат, также принадлежащий полю.  Принятое обозначение поля - GF(),  где 2 называется порядком поля (число элементов поля), n - значность кода. Простейшее поле GF(2) содержит два элемента 0 и 1.

Поле Галуа GF(),  элементами которого являются полиномы степени не выше  n-1, описывает, таким образом, все кодограммы кода значности  n.  Для образования избыточного кода способного обнаруживать или даже исправлять ошибки, возникающие при передаче, необходимо сократить число используемых кодограмм, сохранив значность кода. Оставшиеся  кодограммы называются разрешенными, их число меньше, чем . Выделение разрешенных кодовых комбинаций можно осуществить разными способами. В зависимости от используемого способа, образованный избыточный код обладает разной корректирующей способностью, а устройства кодирования и декодирования – разной степенью сложности. Корректирующая способность кода тем выше, чем больше кодовое расстояние d. Кодовым расстоянием называют минимальное количество разрядов кода, в которых одна кодовая комбинация отличается от другой. В случае двоичного кода кодовое расстояние находят путем суммирования по модулю 2 двух кодовых комбинаций и подсчета числа получившихся едениц.