Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов, страница 5

В разделе 2.3 установлены два алгоритма кодирования, используемые на практике. Первый из них,  определяемый выражением (6), требует выполнения умножения информационного многочлена на одночлен и вычисления остатка от деления произведения на образующий многочлен g(х). Умножение на одночлен не требует специального устройства, так как такое умножение означает приписывание n-k нулей со стороны младших разрядов к кодируемой кодовой комбинации. Эта операция выполняется за счет организации работы датчика. Вычисление остатка осуществляется схемой деления на g(х). Информационные символы с приписанными n-k нулями поступают, начиная со старшего разряда, одновременно в схему деления и в канал связи: Когда все k информационных символов и n-k нулей поступят в канал связи, регистр схемы деления будет содержать остаток, т.е. проверочные символы передаваемой кодограммы. Для вывода их из регистра требуется n-k тактов. Недостаток этого кодера состоит в том, что формируемая кодограмма циклического кода имеет разрыв между информационными и проверочными символами в n-k символов, что снижает скорость передачи информации. Недостаток устраняется использованием специальной схемы деления [1].

Второй тип кодирующих устройств, применяемых на практике, функционирует на основе рекуррентных  соотношений (7) и реализуется в виде регитсра сдвига с  k  ячейками памяти (по числу информационных символов) и логической обратной связью. Информационные символы заносятся в регистр так, чтобы старший коэффициент  оказался  в последней ячейке (см. рис. 2), а  в первой.

Рисунок .2

Логическая обратная связь построена таким образом, что на ее выходе  формируется первый проверочный символ

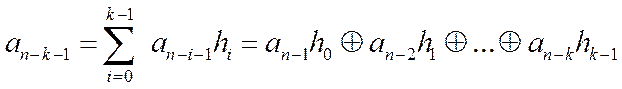
После поступления первого импульса продвижения (цепи, по которым поступают импульсы продвижения, на рис.2 не показаны) этот символ запишется в первую ячейку, а информационные символы сместятся на одну ячейку вправо. Теперь на выходе ЛОС действует второй проверочный символ:

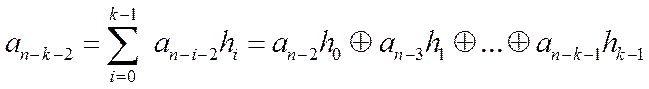
На последующих тактах работы последовательно формируются оставшиеся проверочные символы и затем снова информационные символы.

Рассмотрим подробнее работу кодирующего устройства на примере кодера для кода (7,3), порожденного многочленом . Генераторный многочлен при этом таков: . Соответствующее кодирующее устройство приведено на рис.3.

В исходном состоянии содержимым регистра являются  . Из схемы видно, что проверочный символ есть сумма по mod2 содержимого ячеек 2 и 3. Это позволяет легко вычислить содержимое регистра  на любом такте работы. Результаты вычислений представлены в табл. 1. Из таблицы можно видеть, что после семи тактов работы регистр вновь содержит информационные символы. Следовательно, далее содержимое регистра начинает повторяться и на входе регистра сформируются периодически повторяющаяся кодограмма циклического кода. Из таблицы также установим, что 1саждый символ циклического кода может быть представлен разными линейными соотношениями:

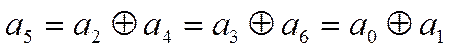                                  (11)

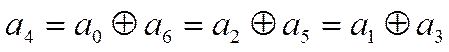
Эти соотношения, называемые проверками используются, при декодировании циклических кодов.

Таблица 1.

Простейшим декодирующим устройством является декодер, обнаруживающий ошибки ( но не исправляющий). Исправление ошибок осуществляется обычно повторной передачей кодограммы по команде декодера. Команда на повторную передачу передается  на передающий конец канала связи по обратному каналу.

Функциональная схема декодирующего устройства, обнаруживающего ошибки приведена на рис.4.