Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов, страница 3

Двучлен разлагается на множители следующим образом:

 (4)

Комбинируя различные сочетания скобок можно получить 28 возможных   образующих многочленов. В этом случае неоднозначность выбора g(x) проявляется ещё сильнее.      

Б. По заданным n и d

В этом случае используется методика, разработанная Боузом, Чоудхури и Хоквингемом. Коды, построенные по этой методике, получили название кодов БЧХ. Порождающий многочлен для кода БЧХ определяется равенством

где НОК- наименьшее общее кратное, r=0 при четном d и г=1 при нечетном d.  - так называемые минимальные функции, или минимальные многочлены .

Минимальные функции являются неприводимыми полиномами и имеют вид [1]:

-для n=7

                  

       

-для n=15

                                  

       

        

     

  

Рассмотрим пример. Пусть требуется построить циклический код с тремя информационными символами (k=3) и кодовым расстоянием d=4. Вычислим образующий многочлен в рассматриваемом примере. Т.к. d имеет четное значение, положим r=0, тогда:

Если проделать то же самое для d =3, то r=1 и

МККТТ - стандартизован циклический код с образующим многочленом

применяемый в настоящее время во многих системах передачи  данных.

2.3. Принципы кодирования и декодирования циклических кодов

Существует три способа кодирования циклических кодов. Наиболее просто кодограммы циклического кода можно получить, умножая соответствующие информационные многочлены  на образующий многочлен g(x):

       (5)

Это правило становится очевидным, если вспомнить, что кодограммы циклического кода образуют идеал, т.е. множество многочленов, кратных образующему. Крупный недостаток этого способа состоит в том, что он приводит к неразделимому коду в которой   коду в котором      информационные и проверочные  символы  не  занимают  постоянных   мест в блоке (кодограмме).

Другой метод образования  кодограмм  циклического кода основан на соотношении

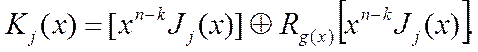         (6)

Нетрудно убедиться, что   делится на g(x)  без остатка и, следовательно, кодограммы (6) образуют  циклический  код.

Пример 1.

Пусть кодированию подлежат       и 

Образующий многочлен     

Согласно (5) имеем

                                             (1110100);

                                                  (0100111);

Правило (6) дает

              ( 1001110);

             (0111010).

Из примера видно, что  правило (5) приводит к неразделимому коду;  в комбинациях, построенных согласно правилу (6),   всегда на первых позициях стоят информационные символы, а на последующих -  проверочные.

Третий способ кодирования основан на том, что циклический код является систематическим (линейным) и его проверочные и информационные символы связаны  линейными  соотношениями. Для использования этого метода кодирования необходимо представить комбинацию циклического кода в другом ви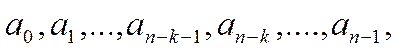де:

 где    - информационная  часть 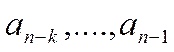 -  проверочная часть.

Можно  показать, что j-й   проверочный символ (в прежнем обозначении или 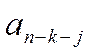в новом),  занимающий  в  кодограмме (n-k-j)-ю   позицию, определяется рекуррентным соотношением:

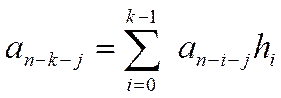                                                                         (7)

где h -   коэффициенты генераторного (проверочного) многочлена

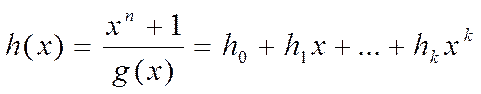
Таким образом, согласно (7) любой символ циклического кода является взвешенной суммой k других символов кода (суммирование выполняется по модулю два).

Пример 2.   Вычислим генераторный (провepoчный) многочлен

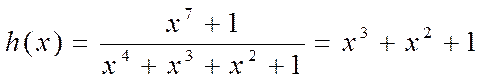
Для информационного многочлена  согласно (7) имеем

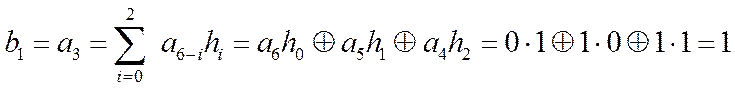
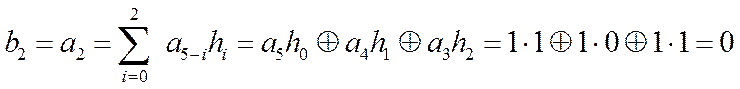
Из примера видно, что проверочные символы  совпадают с соответствующими символами кодового слова в примере 1.

Декодирование циклических кодов может быть осуществлено разными способами. Наиболее простой - это хранить на приемной стороне весь список разрешённых кодовых комбинаций и сравнивать с ними принятую комбинацию. Если она не совладает ни с одной из имеющихся в списке - произошла ошибка. Второй способ заключается в том, что по принятой информационной части кодовой комбинации вычисляются  проверочные  разряды и  сравниваются с принятыми проверочными разрядами. Если они совпадают, то ошибка отсутствует. В противном случае фиксируется наличие ошибки. Оба эти способа могут только выявить факт наличия ошибки, но не позволяют определить ошибочный разряд с целью его корректирования.