Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов, страница 2

Для обнаружения ошибок необходимо, чтобы кодовое расстояние удовлетворяло условию:

где  - кратность обнаруживаемых ошибок.

Для исправления ошибок необходимо, чтобы расстояние от принимаемой с ошибками запрещенной комбинации до переданной было меньше, чем до любой другой разрешенной. Это возможно, если:

где - кратность исправляемых ошибок. В этих выражениях  и  дают число гарантированно обнаруживаемых ошибок.

Один из эффективных способов избыточного кодирования состоит в следующем. Фиксируется некоторый многочлен  g(x) из поля GF(), и выделяются те  многочлены, которые делятся на многочлен g(x) без  остатка.  Выделенное таким образом подмножество поля называется идеалом,  a g(x) - порождающим многочленом идеала.       

Количество различных элементов в идеале и их свойства определяются видом порождающего многочлена. Если, например, за порождающий многочлен взять нулевой элемент, то весь идеал состоит из этого единственного элемента. Если g(x)=1 то в  идеал войдут все многочлены поля. Построенный таким образом код называется полиномиальным.

5. Циклическим называется такой полиномиальный код. который обладает следующим свойством: если комбин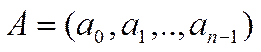ация комбинация циклического кода, то и комбинация  - также комбинация этого кода. Представив комбинации  и в виде многочленов и , нетрудно установить связь между ними в следующем виде (не забывая о правилах приведения подобных членов по модулю два):

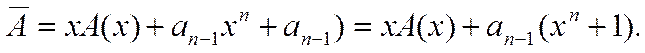(1)

Пусть  A(x) принадлежит идеалу с образующим g(х). Для того, чтобы циклический сдвиг этой комбинации также принадлежал этому идеалу, необходимо деление  многочлена А(x) без остатка на g(x). Из  выражения (1) следует, что это условие будет выполнено в том случае, если двучлен  делится на g(x) без остатка.

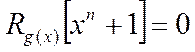       (2)

Полином g(x),  являющийся делителем двучлена , называется образующим многочленом циклического кода. При этом степень

deg[g(x)]=n-k , где k – число информационных символов.

Свойство (2) является отправным при выборе образующего многочлена циклического кода.

2.2. Выбор образующего многочлена циклического (n,k) кода

Выбор образующего многочлена определяет корректирующие способности кода. При этом необходимо учитывать конечное назначение кода. Например, если для обнаружения ошибок необходимо только зафиксировать факт ошибки, то для ее исправления надо определить номер ошибочного разряда. Основой для этих действий является свойство делимости разрешенной кодовой комбинации на образующий многочлен без остатка. Ненулевой остаток от деления ошибочной кодовой   комбинации   на   образующий   многочлен   называют   синдромом.  Возникновение ненулевого остатка является признаком ошибки, а конкретный вид синдрома в ряде случаев однозначно связан с местом возникновения ошибки.  В таком случае для исправления ошибок необходимо выбирать такие образующие многочлены, которые при делении ошибочных комбинаций порождают количество различных остатков, совпадающее с количеством возможных ошибок. В частности,  для исправления одиночной ошибки необходимо, чтобы степень образующего многочлена была связана с  соотношением .   Многочлены, обладающие таким свойством, называют примитивными. Для исправления ошибок с кратностью   необходимо выбирать , где     определяемся из условия . Существует два способа нахождения образующего многочлена.

А. По заданным   и

Выбор образующего многочлена циклического кода производится на основе разложения двучлена  на множители - полиномы с коэффициентами 0 и 1. Рассмотрим эту процедуру на примере. Пусть требуется найти образующий многочлен циклического кода (7,3) (значность кода 7, число информационных символов 3).

Двучлен   разлагается на множители следующим образом:

.         (3)

При этом возможны следующие многочлены:

Поскольку число проверочных символов n-k равно степени образующего многочлена, то требуемый код (7,3) может быть образован многочленом степени 4, т.е.  и .

Как видим, этот метод не обеспечивает однозначного выбора образующего многочлена. При этом корректирующая способность полученных кодов будет, различной.