Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов, страница 7

Каждый такт разделен на два:  содержимое ячеек на под такте "а” вычисляется без учета ЛОС на подтакте "б" учитывается действие ЛОС. В последней колонке записан символ, действующий на выходе делительного устройства и одновременно на входе ЛОС. Отметим, что для вывода ошибочного символа из БР требуется 5 рабочих тактов (кодограмма а'(х) записывается в БР начиная со старшего разряда). Из таблицы можно видеть,   что опознаватель 100 содержится в регистре схемы деления на 5-м такте, т.е. в момент вывода ошибочного символа из БР.

Проверим, выполняется ли это условие для случая ошибки в 5-м разряде, т.е.

 (1111001). Синдром  (110). Из табл.3 можно видеть, что опознаватель 100 содержится в регистре сдвига схемы деления на 3-м дополнительном такте и на этом же такте ошибка выводится, из БР.

Легко убедиться, что для рассматриваемого кода комбинация 100 является опознавателем любой одиночной ошибки (в любом разряде): Описанную процедуру декодирования допускают лишь коды Хемминга, для которых выполняется условие

Таблица 3

КЛС может быть реализована в этом случае в виде схемы "И", один из выводов схемы подключается к прямому выходу ячейки 1, а два других - к инверсным выходам ячеек 2 и 3.

Аналогичным образом можно построить КЛС для исправления ошибок более высокой кратности. Однако сложность таких схем значительна, из-за чего они используются весьма редко.

Последний метод декодирования, рассматриваемый здесь, называется мажоритарным. Он основывается на реализации проверок вида (11)  и подсчете их результатов. Решение о значении проверяемого символа принимается по большинству результатов контрольных проверок (отсюда и название метода - по аналогии с мажоритарной системой голосования).

Система контрольных проверок вида (11), построенная для одного символа, циклического кода,  может быть использована для декодирования  всех символов этой комбинации. Действительно, контрольным проверкам удовлетворяет любая кодограмма циклического кода, а следовательно и кодограммы,  полученные циклическими перестановками исходной.  Таким образом, для декодирования  символа:  достаточно произвести j сдвигов принятой кодограммы, не изменяя ни схемы вычисления проверочных соотношений, ни мажоритарного элемента.

Существует две разновидности мажоритарных декодеров. Рассмотрим пер¬вую из них на примере некоторого циклического кода длиной n=7, для которого проверки имеют вид:

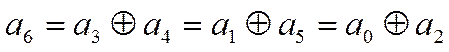
 (12)

Мажоритарный декодер МД-1 первой разновидности представляет собой БP, дополненный устройствами,  реализующими проверки (12) относительно какого-либо одного символа (например, ), и мажоритарным элементом (МЭ). При этом используется и тривиальная проверка (вида 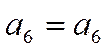). Схема декодера приведена на рис.6. МЭ выносит решение о значении проверяемого символа по большинству результатов проверок, действующих на его входах. Если результаты проверок делятся поровну (например, 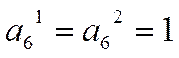 ,  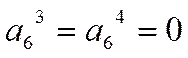 ), то МЭ выдает сигнал, свидетельствующий о наличии неуправляемой ошибки (например, двукратной).