Краткие теоретические сведения о циклических кодах. Изучение принципов кодирования и декодирования циклических кодов, страница 8

В практических схемах вместо МЭ используют пороговый элемент ПЭ, который не фиксирует появление неисправляемой ошибки.

Рисунок 6.

Для проверки остальных символов кода достаточно произвести циклическую перестановку записанной кодограммы. С этой целью переключатель 2 устанавливается в положение 1 и подается импульс сдвига. На рис.6      приведен  результат такого сдвига на один такт. Теперь декодер реализует следующие соотношения: 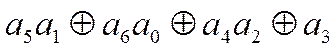. Сравнив их с (12), можно убедиться, что декодер осуществляет проверки относительно символа . Таким образом, для проверки и исправления информационных символов потребуется k тактов работы.

В рассмотренном примере имеется 4 соотношения проверки. Нетрудно заметить, что любая однократная ошибка нарушает только одну контрольную проверку. Следовательно. МЭ исправит однократную ошибку. Двукратные ошибки (ошибки в двух символах кодограммы) не могут быть исправлены (голоса разделяются поровну), но будут обнаружены.

В проверках (12) каждый символ , участвует один раз. Такие проверки, называют разделенными. Следует иметь в виду, что разделенные проверки получаются не всегда, т.е. один или несколько символов могут входить в проверки не один раз. В этом случае и однократная ошибка может нарушать более чем одну проверку.

Мажоритарный декодер МД-2 использует тот факт, что элементы синдрома есть суммы по mod2 определенных символов принимаемой комбинации. Действительно, пусть для некоторого циклического кода генератор синдрома представлен на рис.7.  Формирование синдрома при поступлении кодограммы отображается в табл.4.

На 7-м такте работы схема образует синдром (S1,S2,S3).

Рисунок 7.

Таблица 4.

Причем согласно таблице 4 имеем:

,

,

.

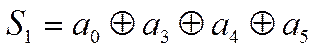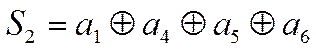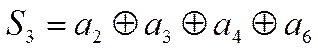Если ошибок нет, то очевидно, что эти суммы равны нулю (нулевой синдром – основной признак отсутствия ошибок). Значит равны нулю суммы:

,

.

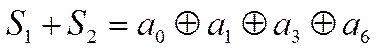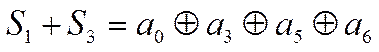Наличие ошибки только в старшем разряде приводит к тому, что последние  4 суммы  оказываются равными единице ( S1=0 т.к. в нее  не входит).

Если же имеет место ошибка в любом другом разряде, то равными единице оказываются только две суммы из четырех. Это обстоятельство можно использовать для исправления ошибки с помощью схемы, приведенной на рис.8. На вход ПЭ подаются четыре суммы: , ,, 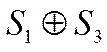Если, проверяемый первым 7-й разряд ошибочен, то все эти суммы равны единице и на выходе ПЭ появится "1" (4>3).

Рисунок 8.

Таким образом, на 8-м такте ошибка 6удет исправлена. При этом синдром должен стать, очевидно, нулевым (так как ошибка однократная и исправлена). Анализируя 8-ю строку табл.4, можно видеть, что содержимое только первой ячейки генератора синдрома отлично от нуля (зависит от , а  и от  не зависят). Суммирование , с “1” на выходе ПЭ (осуществляется связью, показанной на рис. 8 пунктиром) переводит первую ячейку в состояние "0". Вывод остальных символов из БР теперь уже не будет сопровождаться коррекцией.

Если однократная ошибка имеет место в 6-м разряде, то на 8-м такте ПЭ даст отклик "0" и поэтому 7-й символ кодограммы покинет БР без исправления. Синдром также не корректируется, и, следовательно, содержимое генератора синдрома определяется 8-й строкой табл.4.

Ошибочный 6-й разряд обращает все четыре суммы в “1”, а ошибка в любом другом разряде -  только две из них. Следовательно. ПЭ распознает ошибку в 6-м разряде. На последующих тактах работы аналогичным образом проверяются остальные разряды комбинации. 

3. ОПИСАНИЕ МАКЕТА КОДИРУЮЩЕГО УСТРОЙСТВА