Уравнение теплопроводности в неограниченной области.
(1)
Определение. Классическим решением задачи (1) называется функция 
, определённая и непрерывная вместе
со вторыми производными по 
и первыми
производными по 
в области 
, удовлетворяющая уравнению (1) в
этой области, непрерывная по в области 
и удовлетворяющая начальному
условию.
Теорема. Задача (1) может
иметь только одно классическое решение, ограниченное в .
Доказательство. Пусть 
два классических ограниченных
решения задачи 
.
Очевидно 
есть решение задачи
И
кроме того 
Но воспользоваться принципом максимума в неограниченной области нельзя.
Чтобы
воспользоваться принципом максимума, рассмотрим ограниченную по область 
.
Здесь 
будем потом увеличивать.
Введём вспомогательную функцию
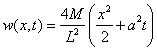
Эта функция удовлетворяет уравнению теплопроводности, кроме того
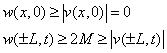
Применяем
принцип сравнения к функциям 
и 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
