Уравнение теплопроводности в неограниченной области, страница 2

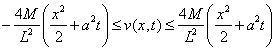
Это справедливо  поэтому фиксируя  и устремляя . Получим

Для решения задачи (1) применим преобразование Фурье с ядром

, ,

,  

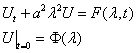
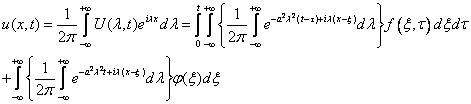
Вычислим интеграл в фигурных скобках

      

    

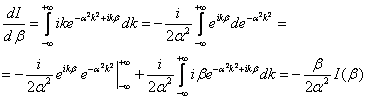
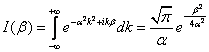
Обозначим

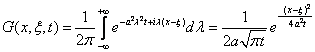
 (2)

Теорема. Если  непрерывна и ограничена на бесконечной прямой  функция, а  не прерывна по совокупности переменных и ограниченна, то формула определяет при  классическое решение задачи (1).

Замечание требование ограниченности и непрерывности может быть ослабленно.

Доказательство теоремы на стр 218. Боголюбов Кравцов, Свешников

Задача для уравнения теплопроводности на полупрямой

Лемма. Пусть функция  определена на бесконечной прямой , имеет на ней ограниченные производные до N-го порядка, и линейная комбинация