![]() ,
,
нечётна
относительно точки ![]() .Тогда функция
.Тогда функция 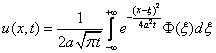
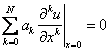
Прежде
всего отметим, что функция Грина 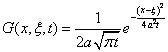
удовлетворяет
условию ![]()
В
силу наложенных на ![]() условий интеграл можно
дифференцировать
условий интеграл можно
дифференцировать
![]()
Интегрируя
по частям, получим ![]()
и
в силу нечётности всей! Подынтегральной функции при ![]() ,
получаем
,
получаем 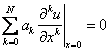 .
.
Способ решения однородного уравнения теплопроводности
![]()
![]()
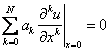
Продолжим
![]() , заданную при
, заданную при ![]() , на всю действительную ось, построив
функцию
, на всю действительную ось, построив
функцию ![]() , которая удовлетворяет условиям
, которая удовлетворяет условиям ![]() .
.
![]()
Теперь решим задачу Коши на прямой.
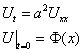
Очевидно, это решение будет решением на полупрямой.
Задача
Дирехле ![]()

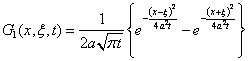
Решение неоднородной задачи
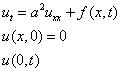
![]()
Для задачи Неймана
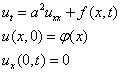
![]()
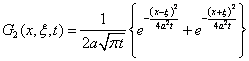
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.