Уравнение Гельмгольца
Принцип максимума для уравнения ![]() .
.
Теорема. Решение уравнения ![]() ,
определённое и непрерывное в замкнутой области, не может достигать во
внутренних точках области положительных максимальных и отрицательных
минимальных значений
,
определённое и непрерывное в замкнутой области, не может достигать во
внутренних точках области положительных максимальных и отрицательных
минимальных значений
Доказательство.
Пусть ![]() , тогда
, тогда ![]() ,
,![]() ,
,![]() откуда
откуда
![]()
Но в этом случае в правой части уравнения стоит отрицательное число, т.е. ур-е не выполнено. Это предположение показывает, что исходное уравнение не верно.
Фундаментальное решение.
Трёхмерный случай.
![]()
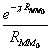
![]()
Ситуация сложнее
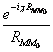 ,
,![]() ,
,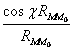 и любое из этих решений можно взять
как фундаментальное.
и любое из этих решений можно взять
как фундаментальное.
Двумерный случай
![]()
![]()
![]()
![]() ,
, ![]() ,
,
![]()
В ограниченной области можно брать любое в неограниченной выбор фундаментального решения определён выбором условия на бесконечности.
Для вывода третьей формулы Грина для оператора Гельмгольца необходимо провести те же, выкладки, что и для оператора Лапласа.
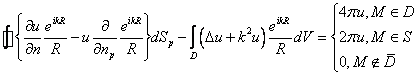
Таким образом сразу получаем интегральное представление
![]()
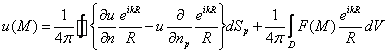
Краевые задачи
Внутренняя задача Дирихле для уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.