Уравнение Гельмгольца, страница 2

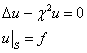
Теорема. Задача Дирихле не может иметь более одного классического решения.

Доказательство.

В силу линейности достаточно доказать, что

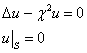
имеет только тривиальное решение. Но в силу принципа максимума , и , т.е

.

Задача Неймана и третья краевая задача.

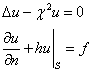
Теорема. При  на  краевая задача не может иметь более одного классического решения.

Доказательство. Достаточно показать, что однородная задача имеет только тривиальное решение

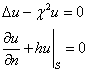
Воспользуемся первой формулой Грина.

Т.к.

Примечание. Если знак  будет другим, то однородная задача может иметь и нетривиальные решения.

Краевые задачи для уравнения

Внутренние краевые задачи могут иметь неединственное решение, если  совпадёт с собственным значение для оператора Лапласа для этой области. В этом случае решения неоднородной задачи может вообще не быть либо оно будет определяться неоднозначно.

Функция Грина.

Рассмотрим следующую задачу Дирихле

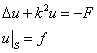
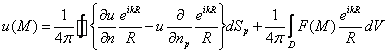
Пусть  решение

Применяя к  и  вторую формулу Грина.