![]() Лекция
3. Специальные функции.
Лекция
3. Специальные функции.
В предыдущей лекции мы рассмотрели некоторые физические задачи, приводящие к уравнениям в частных производных, а так же обсудили их классификацию. Уравнения каждого типа обладают рядом специфических свойств. Однако существуют и общие методы решения применимые для уравнения всех типов. Один из таких методов – метод разделения переменных или метод Фурье. Прежде чем изложить метод разделения переменных решения начально-краевых задач, при котором естественно возникает необходимость рассмотрения специальных функций, являющихся решением задач Штурма-Лиувиля, изучим свойства наиболее часто встречающихся спец.функций.
1. Цилиндрические функции.
Уравнением Бесселя или уравнением цилиндрических функций, называется уравнение вида
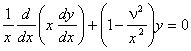 (1)
(1)
![]() .
.
Напомним свойства гамма-функции.
Гамма-функцией называется интеграл
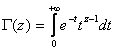
![]() - комплексное число, реальная часть
которого положительна.
- комплексное число, реальная часть
которого положительна.
а)
![]() ,
, ![]() .
.
б)
![]() , если
, если ![]() -натуральное
число, то
-натуральное
число, то ![]()
в)
![]()
![]()
Подставляя
это выражение в уравнение (1) и приравнивая коэффициенты при одинаковых
степенях ![]() , получим следующие рекуррентные
соотношения
, получим следующие рекуррентные
соотношения
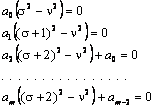
Из
первого уравнения следует, что ![]() , рассмотрим
случай
, рассмотрим
случай ![]() , тогда
, тогда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.