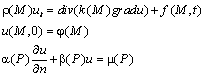
Определение. Классическим решением начально-краевой задачи
называется функция , непрерывная вместе с
первыми производными по координатам в замкнутом цилиндре, имеющая непрерывные
производные первого порядка по и второго по
координатам в открытом цилиндре, удовлетворяющая уравнению, начальному условию
и граничному условию.
Необходимым
условием существования классического решения начально-краевой задачи является
условие согласования начального и граничного условия.
Принцип
максимума.
Решение однородного уравнения теплопроводности
непрерывное в замкнутом цилиндре во внутренних точках
этого цилиндра не может принимать значений, больших, чем максимальное из
начального и граничного значений.
Доказательство
Нужно
доказать, что если
То
От
противного
Пусть
в некоторой внутренней точке функция достигает своего максимального
значения, т. е.
Введём
вспомогательную функцию.
если
Т.к.
функция непрерывна в замкнутом цилиндре, то
она должна в некоторой внутренней () достигать
своего максимального значения, тогда
, непрерывная вместе с
первыми производными по координатам в замкнутом цилиндре, имеющая непрерывные
производные первого порядка по 
и второго по
координатам в открытом цилиндре, удовлетворяющая уравнению, начальному условию
и граничному условию. 
функция 
если 
непрерывна в замкнутом цилиндре, то
она должна в некоторой внутренней (
) достигать
своего максимального значения, тогда 
выполняются условия максимума 
